
| Online Judge | Online Exercise | Online Teaching | Online Contests | Exercise Author |
|
F.A.Q Hand In Hand Online Acmers |
Best Coder beta VIP | STD Contests DIY | Web-DIY beta |
成长,生命,幸福
Time Limit: 4000/2000 MS (Java/Others) Memory Limit: 524288/262144 K (Java/Others)Total Submission(s): 1208 Accepted Submission(s): 385
Problem Description
Alice作为德鲁伊,有一棵神奇的树,这棵树会不断的成长。
对于一个节点$i$的成长,先将这个节点变为$d_i$边型($d_i$为这个点的度数),然后将原本与这个点相连的边随机匹配多边形上的点,再随机删除由这个点变化成的多边形上的一条边。
特别的,对于一个度数为$0$或$1$的点,进行成长将不会发生变化。
对于一棵树的成长,定义为树上所有的节点进行一次成长。
Alice认为一棵树的直径越长,长得越好,所以Alice想要知道,在这棵树进行$m$次成长后,直径的长度最大可能是多少。
这里定义树的直径的长度为直径上的点数。
答案对$10^9+7$取模。
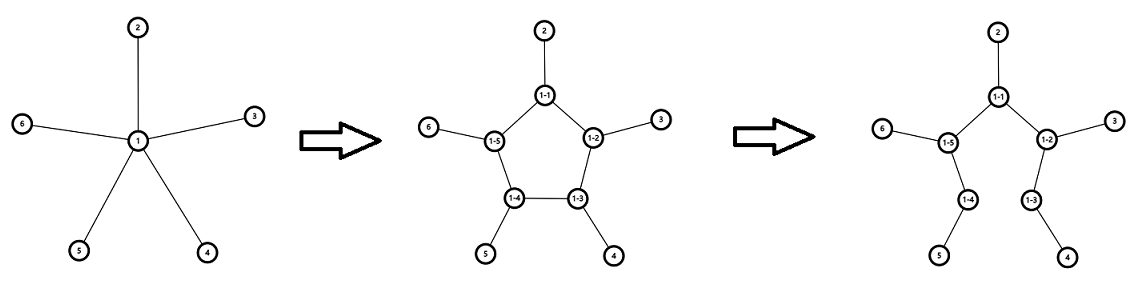
对于一个节点$i$的成长,先将这个节点变为$d_i$边型($d_i$为这个点的度数),然后将原本与这个点相连的边随机匹配多边形上的点,再随机删除由这个点变化成的多边形上的一条边。
特别的,对于一个度数为$0$或$1$的点,进行成长将不会发生变化。
对于一棵树的成长,定义为树上所有的节点进行一次成长。
Alice认为一棵树的直径越长,长得越好,所以Alice想要知道,在这棵树进行$m$次成长后,直径的长度最大可能是多少。
这里定义树的直径的长度为直径上的点数。
答案对$10^9+7$取模。

Input
第一行包含一个整数$T$($1 \leq T \leq 5$),表示数据组数
每组数据的第一行包含两个整数$n,m$($1 \leq n \leq 10^5,1\leq m \leq 10^9$),表示一棵$n$个节点的树,进行$m$次成长
接下来$n-1$行,每行包含两个整数$u,v$($1 \leq u,v \leq n$),表示树上的一条边
每组数据的第一行包含两个整数$n,m$($1 \leq n \leq 10^5,1\leq m \leq 10^9$),表示一棵$n$个节点的树,进行$m$次成长
接下来$n-1$行,每行包含两个整数$u,v$($1 \leq u,v \leq n$),表示树上的一条边
Output
一共$T$行,每行一个整数,表示第$i$棵树成长后的最大直径。
Sample Input
2 5 1 1 2 1 3 3 4 3 5 7 3 1 2 1 3 2 4 2 5 2 6 3 7
Sample Output
7 40
Source
| Home | Top |
Hangzhou Dianzi University Online Judge 3.0 Copyright © 2005-2025 HDU ACM Team. All Rights Reserved. Designer & Developer : Wang Rongtao LinLe GaoJie GanLu Total 0.000000(s) query 1, Server time : 2025-04-01 07:36:04, Gzip enabled |
Administration |