梦中的地牢战斗

众所周知，小凯是一个网瘾少年，这天梦里，他又梦到了自己在玩一款游戏——

在一张 $ n\times m $ 大小的地牢里（左下角为 $ (1,1) $ ，右上角为 $ (n,m) $ ），有 $ K $ 个怪物，小凯操控着主角为了获取收益来进入地牢猎杀这些怪物。

对于每个怪物有这样三个属性，价值 $ A_i $ ，攻击力 $ B_i $ ，攻击距离 $ C_i $ 。

$ \textbf{主角的初始生命值为1} $，在进入地牢前，你会有一个商店供你购买生命值，你可以贷款 $ x $ 个金币（ $ x $ 为任意正整数）来获得 $ x $ 点生命值，当然你也可以选择不贷款。注意你只能在进入地牢前购买生命值，进入地牢后将无法购买生命值。

一开始，主角会出现在地图的 $ (sx,sy) $ 位置，保证该位置上没有怪物。

在每回合的开始，主角可以进行下面两个操作中的一个操作。

1.离开地牢，获得当前击杀怪物的金币并进行结算。

2.瞬移到$ \textbf{同行/同列} $上与当前位置距离不超过 $ d $ 的$ \textbf{没有怪物的地图内的位置} $，并且消灭瞬移起点和终点相连的线段上的所有怪物。（消灭怪物可以瞬间获得怪物的价值数量的金币）这里的距离可以用曼哈顿距离来理解。

在每回合结束时，会结算怪物对主角造成的伤害。（死亡的怪物不会对主角造成伤害）

对于每个怪物而言，如果主角和怪物之间的曼哈顿距离$ \textbf{小于等于} $怪物的攻击距离 $ C_i $ ，那么主角就会受到 $ B_i $ 点伤害。在任意时刻主角的生命值$ \textbf{小于等于0} $角色就会死亡，并且$ \textbf{失去所有获得的金币} $。

试问主角最多能获得多少金币。（最后收益为击杀怪物获得金币减去一开始贷款购买的生命值的花费）

曼哈顿距离的定义如下，对于点 $ S(x_1,y_1) $ 和点 $ T(x_2,y_2) $ ，他们的曼哈顿距离为 $ |x_1-x_2|+|y_1-y_2| $

第一行有一个整数，$ T $ （$ 1 \leq T \leq 15 $) ，代表数组组数

每组数据第一行有三个整数， $ n，m，K $ （$ 2 \leq n,m \leq 30 $，$ 1 \leq K \leq 10 $）

第二行是一个整数， $ d $ （$ 1 \leq d \leq 8 $），代表瞬移的距离上限

接下来有$ K $行，每行有五个整数 $ X_i,Y_i,A_i,B_i,C_i $ 。其中 $ X_i,Y_i $ 表示怪物现在所在点$ (X_i,Y_i) $ , $ A_i,B_i,C_i $分别表示怪物$ i $的价值、攻击力和攻击距离。（$ 1\leq X_i \leq n,1\leq Y_i \leq m , 1\leq A_i,B_i \leq 10^4,1\leq C_i \leq 8 $）

最后一行两个整数 $ sx,sy $ 表示主角一开始在的位置。（$ 1 \leq sx \leq n,1 \leq sy \leq m $）​

对于每组数据输出一行一个整数代表最多可以获得的收益。

1
4 5 2
3
1 4 4 3 2
4 4 7 2 3
1 5

9

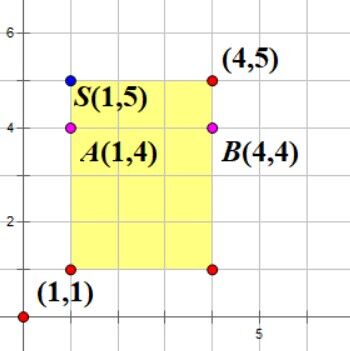
对于样例1而言，其中一种最优策略如下：

我们一开始贷款2，让主角在进入地牢前生命值达到3。

1：主角一开始在 $ S(1,5) $ ，我们可以先瞬移到 $ (1,2) $ ，解决掉 $ (1,4) $ 所在的敌人，获得4枚金币

此时场上只剩下在点 $ (4,4) $ 的怪物，因为 $ (1,2) $ 和 $ (4,4) $ 的曼哈顿距离为5，所以主角不会受到伤害

2：主角从 $ (1,2) $ 瞬移到 $ (4,2) $

因为 $ (4,2) $ 和 $ (4,4) $ 的曼哈顿距离为2，小于怪物2的攻击距离3,所以主角会受到2点伤害

3：主角从 $ (4,2) $ 瞬移到 $ (4,5) $ ，解决掉 $ (4,4) $ 所在的敌人，获得7枚金币

没有怪物存在场上，所以主角不会受到伤害

4：离开地牢，结算收益

我们最后的答案就是-2+4+7=9

2024“钉耙编程”中国大学生算法设计超级联赛（2）