流量监控

在云安全中，网络的流量监控是一个重要问题。

现在有一个 $n$ 个节点，$n-1$ 条链路组成的连通网络结构。通俗的来讲，这是一棵树，其中 $1$ 号节点是网络流量起始节点，或者说，是这棵树的根。

为了对网络上的流量进行合理监控，我们计划在这 $n$ 个节点每个节点都安装一个监控器，并对所有节点进行匹配，每对匹配 $(u,v)$ 将监控节点 $(u,v)$ 之间的流量信息。

一棵树的一个合法匹配方案是指将 $n$ 个节点划分为 $\frac n 2$ 对匹配 $(a_1,b_1),(a_2,b_2),\ldots, (a_{\frac n 2},b_{\frac n 2})$ 并且每个节点恰好出现一次。

并且由于某些技术原因，为了满足安全要求，必须要保证对于每一对匹配 $(u,v)$，$u,v$ 之间有祖孙关系，即一个点在另一个的子树内。

现在，为了对于流量监控做出合理的规划，我们希望求出有多少种满足安全条件的合法监控匹配方案。

例如，图 1 展示了一个满足安全要求的合法匹配方案 $(1,4)$ 和 $(2,3)$。但是图 2 的匹配方案 $(1,2),(2,3)$ 由于 $2$ 出现了多次，是不合法的匹配（当然，奇数个点的树一定没有合法匹配方案）。图 3 则展示了一个不满足安全要求的合法匹配方案，因为匹配 $(3,4)$ 之间并没有祖孙关系。



我们认为两个匹配方案不同当且仅当存在某个点 $u$，在一个方案中匹配 $v$，并在另一个方案中匹配另一个不为 $v$ 的点。

当然，问题不止这一个，为了对于规划的匹配方案做出合理的评估，我们希望对于所有监控方案，求出每个方案中监控匹配的交点个数，对于一个匹配方案，我们认为该方案中某两个不同匹配 $(a,b)$（$a$ 是 $b$ 的祖先），$(c,d)$（$c$ 是 $d$ 的祖先）有一个交点当且仅当这四个点在同一条到叶节点的链上且交错排列，即 $a$ 是 $b,c,d$ 的祖先，$c$ 是 $b,d$ 的祖先，$b$ 是 $d$ 的祖先。

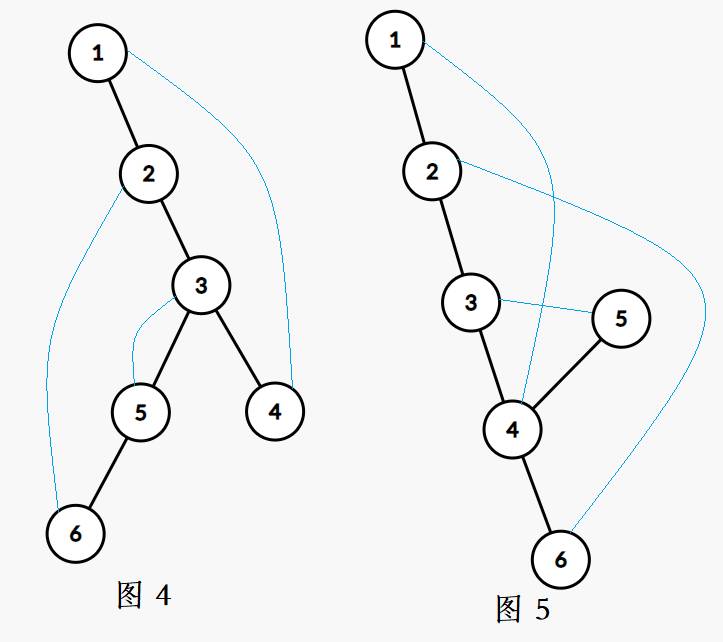
例如，图 4 中的匹配方案并没有交点，因为对匹配 $(1,4),(2,6)$，$4$ 和 $6$ 没有祖孙关系，同样匹配 $(1,4),(3,5)$ 中 $4,5$ 两个点没有祖孙关系，匹配 $(2,6),(3,5)$ 则并没有在一条链上交错排列。而图 5 中的匹配方案有两个交点，由 $(1,4),(3,5)$ 和 $(1,4),(2,6)$ 产生。



由于方案太多了，所以我们只希望你求出所有满足安全条件的合法监控匹配方案的交点个数之和。

由于答案可能会很大，所以只需要输出答案对 $998244353$ 取模的结果即可。

第一行包含一个整数 $T$（$1\le T\le 20$），表示测试用例的组数。

对于每组测试用例，第一行包含一个整数 $n$（$1\le n \le 2000$），表示节点的数量。

接下来的 $n-1$ 行，每行包含两个整数 $u,v$（$1 \le u,v \le n$），表示树的一条边。保证输入构成一棵树。

保证在所有测试用例中 $n$ 的总和不会超过 $20000$。

对于每组测试用例，输出一行两个整数表示满足安全条件的合法监控匹配的方案数和所有满足安全条件的合法监控匹配的方案的监控匹配的交点个数之和，两个数之间用空格分隔，对 $998244353$ 取模。

3
6
1 2
2 3
3 4
3 5
4 6
8
1 2
2 3
3 4
3 5
5 6
5 7
7 8
1

9 4
27 13
0 0

2023 CCPC 华为云计算挑战赛