foreverlasting and fried-chicken

As we all know, There are two ACM heros known as foreverlasting and fried-chicken in BIT. They are immersed in perfect love respectively. The following link tells the love story of fried-chicken.

https://www.zhihu.com/question/62332494/answer/3076483871

Pedestrian1 likes graph and mathematics. He needs your help to solve an easy problem. You are given a simple undirected graph named "fried-chicken" with $n$ nodes and $m$ edges. Please note that the graph is not necessarily connected. The nodes are labeled from $1$ to $n$.

Pedestrian1 wants to know how many "foreverlasting" graphs in the "fried-chicken" graph.



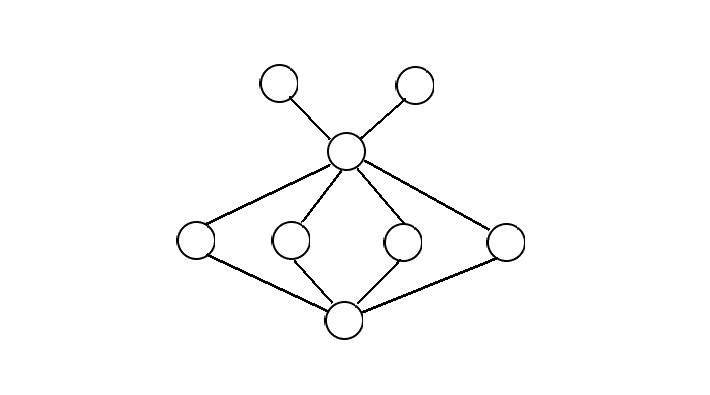
The above image defines a "foreverlasting" graph.

Please note that two "foreverlasting" graphs are considered different when there is at least one different edge between the two edge sets that make up the two "foreverlasting" graphs.

In other word, the given graph is $G(V,E)$. You need to calculate the number of subgraphs $G'(V',E')(V' \subseteq V,E'\subseteq E)$ which satisfy $V'=\\{v_1,v_2,v_3,v_4,v_5,v_6,v_7,v_8\\},E'=\\{(v_1,v_3),(v_2,v_3),(v_3,v_4),(v_3,v_5),(v_3,v_6),(v_3,v_7),(v_4,v_8),(v_5,v_8),(v_6,v_8),(v_7,v_8) \\}$

Since the answer may be very large, Pedestrian1 wants to know the answer modulo $1000000007$.

The first line of input contains the integer $T$ ($1\leq T\leq 10$), the number of test cases. The description of test cases follows.

The first line of each test case contains two integers, $n$ and $m$ ($1\leq n\leq 1000, m\leq \frac {n(n-1)}2$) — the number of nodes and the number of edges, respectively.

Each of the next $m$ lines contains the description of an edge. Each line contains two integers $u_i$ and $v_i$ ($1\leq u_i,v_i\leq n, u_i\neq v_i$) — an edge connects node $u_i$ to node $v_i$.

It is guaranteed that no two edges connect the same unordered pair of nodes.

Furthermore, it is guaranteed that the sum of $n$ over all test cases both do not exceed $3000$.

For each testcase, output an integer representing the answer modulo $1000000007$.

1
8 10
1 2
1 3
1 4
1 5
1 6
1 7
8 4
8 5
8 6
8 7

1

The scanf function may cause Time Limit Exceeded. Please use std::cin and disable the synchronization between the C and C++ standard streams, or consider using a faster input method.

2023“钉耙编程”中国大学生算法设计超级联赛（2）