Cyber Painter

In the world of Cyberpunk, all paintings are done by using lasers. As a cyber painter, painting with lasers is your daily job.

You have a laser painting board with $n$ rows and $m$ columns of laser emitters. The distance between rows is $1$, and so is the distance between columns. Each laser emitter can emit a laser with a length of $0.5$ in four directions. Specifically, you can set an integer between $0$ and $15$ as the state value for each laser emitter, which can be denoted by a four-bit binary number $(X_1X_2X_3X_4)_2$ (For example, $11=(1011)_2$). The meaning of the state value is as follows:

• $X_1=1$: The laser emitter emits a laser of length $0.5$ in the upward direction.
• $X_2=1$: The laser emitter emits a laser of length $0.5$ in the right direction.
• $X_3=1$: The laser emitter emits a laser of length $0.5$ in the downward direction.
• $X_4=1$: The laser emitter emits a laser of length $0.5$ in the left direction.

Given $n \times m$ integers between $0$ and $15$, you need to assign an integer to each laser emitter as its state value. You are curious about the expectation of the number of squares that can be formed by the laser if the $n \times m$ integers are assigned uniformly at random, where the squares can be of arbitrary edge length.

The first line contains an integer $T$ ($1 \le T \le 10^4$), indicating the number of test cases.

The first line of each test case contains two integers $n$ and $m$ ($1 \le n \times m \le 10^5$), indicating the number of rows and columns of the laser emitters.

The second line of each test case contains $16$ integers $a_0,a_1,\dots,a_{15}$ ($0\le a_i\le n\times m$, $\sum_{i=0}^{15}a_i=n \times m$), where $a_i$ indicates the number of integer $i$.

It guaranteed that the sum of $n\times m$ over all test cases won't exceed $10^6$.

For each test case, output the expectation of the number of squares that can be formed by the laser in a single line. You should output the answer modulo $10^9+7$. Formally, let $M=10^9+7$. It can be shown that the answer can be expressed as an irreducible fraction $\frac{p}{q}$, where $p$ and $q$ are integers and $q\not\equiv 0\pmod M$. Output the integer equal to $p \times q^{-1}\bmod M$. In other words, output such an integer $x$ that $0 \le x < M$ and $x \cdot q \equiv p \pmod M$.

3
2 2
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 4
2 2
0 0 0 1 0 0 1 0 0 1 0 0 1 0 0 0
3 3
0 0 0 0 0 0 1 0 0 1 0 1 1 1 2 2

1
41666667
41699736

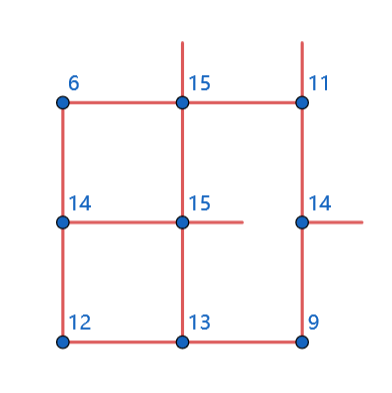
For the third test case in the sample, the following picture shows a possible assignment, which forms $3$ squares.

2022“杭电杯”中国大学生算法设计超级联赛（7）