Occupying Grids

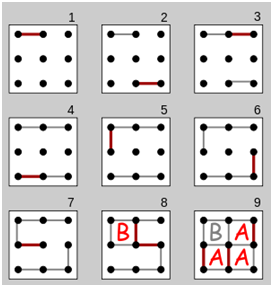
Little Rabbit and Little Horse are playing a game called $\textit{Occupying Grids}$. The game is played on a square grid graph which has $m$ dots each row and $n$ dots each column. The players take turns to draw a segment that connects two adjacent dots. Once the four sides of a grid are all drawn, the player who draws the last side of the grid can occupy the grid and $\textbf{immediately}$ get one more chance to draw another segment. (Sometimes two grids can be occupied at the same time, but the player also gets $\textbf{only one}$ more chance to draw.) The game ends when no more segments can be drawn, and the player who occupies more grids will win the game. (Two players occupying the same number of grids results in a tie.) The picture below shows a game in a $3 \times 3$ square grid graph.






Little Rabbit and Little Horse both play the game for the first time. So in the beginning, they just draw the segments willy-nilly without any strategies. But after $k$ steps, they are surprised to find that each grid has $\textbf{at least 2}$ sides that are drawn. Little Rabbit wants to know whether he can win the game if both players play optimally from now on.

Little Rabbit cannot solve the problem, so he turns to you and shows you the $k$ steps $\textbf{in order}$. But he forgets to note down which player each step belongs to, so you need to judge by yourself. The only thing you know is that the first step belongs to Little Rabbit.

Please note that the $k$ steps given should strictly follow the rules. For example, if one player occupies a grid in some step, then the next step also belongs to him.

The first line of the input contains an integer $T$ ($1 \le T \le 50$), indicating the number of test cases.

The first line of each test case contains three integers $n,m,k$ ($2 \le n,m \le 100$, $1 \le k \le 2nm-n-m$), indicating the number of rows and columns of the square grid graph, and the number of steps Little Rabbit shows you.

Then in the next $k$ lines, each line contains three integers $x,y,o$ ($1 \le x \le n$, $1 \le y \le m$, $0 \le o \le 1$) to describe a step. Here we use $(x,y)$ to describe the point in the $x$-th row and the $y$-th column.

- $\texttt{x y 0}$ ($1 \le x \le n$, $1 \le y < m$): a segment that connects $(x,y)$ and $(x,y+1)$.
- $\texttt{x y 1}$ ($1 \le x < n$, $1 \le y \le m$): a segment that connects $(x,y)$ and $(x+1,y)$.

The first step belongs to Little Rabbit. It is guaranteed that after the $k$ steps, each grid has at least $2$ sides that are drawn. It is also guaranteed that any two steps are different.

For the $x$-th test case, if Little Rabbit wins, output $\texttt{Little Rabbit}$ in a single line. If Little Horse wins, output $\texttt{Little Horse}$ in a single line. If the game ends in a tie, output $\texttt{Tie}$ in a single line.

3
3 3 8
1 1 0
1 2 0
2 1 0
2 2 0
3 1 0
3 2 0
1 3 1
2 1 1
3 3 8
1 1 0
1 1 1
1 2 0
1 3 1
2 1 1
2 3 1
3 1 0
3 2 0
3 3 6
1 1 0
1 2 0
2 1 0
2 2 0
3 1 0
3 2 0

Little Rabbit
Little Horse
Tie

We use solid lines to indicate Little Rabbit's step and dashed lines to indicate Little Horse's step. The first test case of the sample input can be shown as follow.



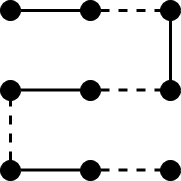
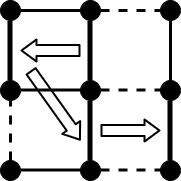
And now it is Little Rabbit's turn. It's obvious that Little Rabbit can occupy all the grids by the following steps.



The second test case of the sample input can be shown as follow.



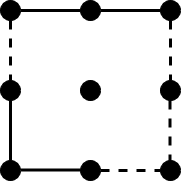
And now it is Little Rabbit's turn. He has no choice but to draw one of the four sides in the middle. Then Little Horse can occupy all the grids.

2021中国大学生程序设计竞赛（CCPC）- 网络选拔赛（重赛）