
| Online Judge | Online Exercise | Online Teaching | Online Contests | Exercise Author |
|
F.A.Q Hand In Hand Online Acmers |
Best Coder beta VIP | STD Contests DIY | Web-DIY beta |
Depth First Search
Time Limit: 20000/12000 MS (Java/Others) Memory Limit: 262144/262144 K (Java/Others)Total Submission(s): 21 Accepted Submission(s): 4
Problem Description
Kris has a rooted tree whose root is $1$. As a master of tree data structure, Kris will dfs the tree. In order to eliminate ambiguity, for each node she will visit its children from left to right. Then she defines $first(x, i)$ as the first node she visited in the subtree of $x$ whose distance to $x$ is $i$. Initially, the tree only has a root node numbered $1$. However, the tree will vary over time and you should maintain $Q$ opeartions, and each operation has one of the following format:
- $1$ $x$ $y$ $z$ $(2 \leq x \leq Q + 1)$, add a leaf node numbered $x$ as a child of $y$ and right subling of $z$. If $z = 0$, you should regard $x$ as the first child of $y$. It is guaranteed that $x$ is unique in every operation and $z$ is a child of $y$ at this moment.
- $2$ $x$ $(x \neq 1)$, remove a leaf node numbered $x$. It is guaranteed that $x$ doesn't have any child at this moment.
- $3$ $x$ $d$ $(d \geq 0)$, Let's define $A = \sum\limits_{i=0}^{d} first(x, i)$, $B = \max\limits_{i=0}^{d} \{first(x, i)\}$. You should output $A$ and $B$ seperated by space. It is guaranteed that $d$ is no more than the height of $x$'s subtree (There exists at least one node in the subtree of $x$ whose distance to $x$ is $d$).
Input
This problem contains multiple test cases.
The first line of the input contains an integer $T$ $(1 \leq T \leq 10)$, representing the number of testcases.
For each testcase, the first line contains an integer $Q$ $(1 \leq Q \leq 2 \times 10^5)$, representing the number of operations.
Then $Q$ lines follow, each line represents an operation. And the operations will be encrypted. You need to decode the operations as follows, where key denotes the value of $A \bmod B$ of the last type $3$ operation and is initially zero for each test case:
It is guaranteed that $\sum Q \leq 1.5 \times 10^6$.
The first line of the input contains an integer $T$ $(1 \leq T \leq 10)$, representing the number of testcases.
For each testcase, the first line contains an integer $Q$ $(1 \leq Q \leq 2 \times 10^5)$, representing the number of operations.
Then $Q$ lines follow, each line represents an operation. And the operations will be encrypted. You need to decode the operations as follows, where key denotes the value of $A \bmod B$ of the last type $3$ operation and is initially zero for each test case:
- For type $1$ operation, let $x = x \oplus key, y = y \oplus key, z = z \oplus key$.
- For type $2$ operation, let $x = x \oplus key$.
- For type $3$ operation, let $x = x \oplus key, d = d \oplus key$. Then you should calculate and output $A = \sum\limits_{i=0}^{d} first(x, i)$, $B = \max\limits_{i=0}^{d} \{first(x, i)\}$, after that set $key = A \bmod B$.
It is guaranteed that $\sum Q \leq 1.5 \times 10^6$.
Output
For each operation of type $3$, output two integers seperated by space indicating the answer.
Example explanation:
After the first $5$ operations, the tree will look like this:
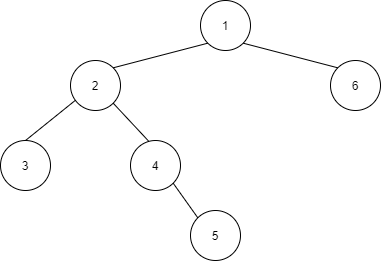
When we dfs the tree, we will visit nodes in the following order:
$$
1, 2, 3, 4, 5, 6
$$
For the $6$th operation, the answer is $A = \sum\limits_{i=0}^{3} first(1, i) = 1 + 2 + 3 + 5 = 11$ and $B = \max\limits_{i=0}^{3} \{first(1, i)\}$ $ = \max\{1,2,3,5\} = 5$.
For the $7$th operation, the answer is $A = 6$, $B = 6$.
After the $8$th operation, the node $3$ is removed and the new tree will look like this:
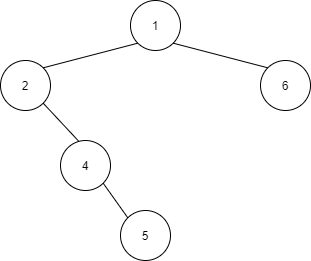
Then, for the last operation, the answer is $A = \sum\limits_{i=0}^{3} first(1, i) = 1 + 2 + 4 + 5 = 12$ and $B = \max\limits_{i=0}^{3} \{first(1, i)\}$ $ = \max\{1,2,4,5\} = 5$.
Example explanation:
After the first $5$ operations, the tree will look like this:

When we dfs the tree, we will visit nodes in the following order:
$$
1, 2, 3, 4, 5, 6
$$
For the $6$th operation, the answer is $A = \sum\limits_{i=0}^{3} first(1, i) = 1 + 2 + 3 + 5 = 11$ and $B = \max\limits_{i=0}^{3} \{first(1, i)\}$ $ = \max\{1,2,3,5\} = 5$.
For the $7$th operation, the answer is $A = 6$, $B = 6$.
After the $8$th operation, the node $3$ is removed and the new tree will look like this:

Then, for the last operation, the answer is $A = \sum\limits_{i=0}^{3} first(1, i) = 1 + 2 + 4 + 5 = 12$ and $B = \max\limits_{i=0}^{3} \{first(1, i)\}$ $ = \max\{1,2,4,5\} = 5$.
Sample Input
1 9 1 2 1 0 1 3 2 0 1 4 2 3 1 5 4 0 1 6 1 2 3 1 3 3 7 1 2 3 3 1 3
Sample Output
11 5 6 6 12 5
Source
| Home | Top |
Hangzhou Dianzi University Online Judge 3.0 Copyright © 2005-2024 HDU ACM Team. All Rights Reserved. Designer & Developer : Wang Rongtao LinLe GaoJie GanLu Total 0.000000(s) query 1, Server time : 2024-11-22 07:19:02, Gzip enabled |
Administration |