
| Online Judge | Online Exercise | Online Teaching | Online Contests | Exercise Author |
|
F.A.Q Hand In Hand Online Acmers |
Best Coder beta VIP | STD Contests DIY | Web-DIY beta |
The Struggle
Time Limit: 7000/7000 MS (Java/Others) Memory Limit: 524288/524288 K (Java/Others)Total Submission(s): 31 Accepted Submission(s): 5
Problem Description
nocriz is a student who, like many, has a dream for his life. Unfortunately, life isn't always easy and there are times when the dream seems faraway and the pursuit feels difficult.
Reality often drives people away from their pursuit of dreams to settle for what they have at hand. Lured to set aside the struggle, nocriz said to Artemisia, "But I shouldn't give up the dream, right?". Artemisia replied: "Of course one should not give up the dream easily! Struggle, struggle until crushed by the rock!".
That night, nocriz had a very bad dream. In his dream there was a rock in the shape of an ellipse, and he was asked to calculate the value $\sum (x \oplus y)^3x^{-2}y^{-1} \mod 10^9+7$ for all integer points $(x,y)$ in the ellipse, where $\oplus$ is the bitwise XOR operation.
In more formal words, you are given integers $a,b,c,d,e,f$, and you are required to calculate $\sum_{(x,y) \in E} (x \oplus y)^3x^{-2}y^{-1} \mod 10^9+7$ where $E = \{(x,y)| x,y \in \mathbb{Z},a(x-b)^2+c(y-d)^2+e(x-b)(y-d) \le f\}$. It is guaranteed that all such points satisfy $0 < x,y < 4 \times 10^6$ and that the ellipse contains at least one integer point.
nocriz was not crushed by the rock that day. Can you solve this problem, like nocriz did?
Reality often drives people away from their pursuit of dreams to settle for what they have at hand. Lured to set aside the struggle, nocriz said to Artemisia, "But I shouldn't give up the dream, right?". Artemisia replied: "Of course one should not give up the dream easily! Struggle, struggle until crushed by the rock!".
That night, nocriz had a very bad dream. In his dream there was a rock in the shape of an ellipse, and he was asked to calculate the value $\sum (x \oplus y)^3x^{-2}y^{-1} \mod 10^9+7$ for all integer points $(x,y)$ in the ellipse, where $\oplus$ is the bitwise XOR operation.
In more formal words, you are given integers $a,b,c,d,e,f$, and you are required to calculate $\sum_{(x,y) \in E} (x \oplus y)^3x^{-2}y^{-1} \mod 10^9+7$ where $E = \{(x,y)| x,y \in \mathbb{Z},a(x-b)^2+c(y-d)^2+e(x-b)(y-d) \le f\}$. It is guaranteed that all such points satisfy $0 < x,y < 4 \times 10^6$ and that the ellipse contains at least one integer point.
nocriz was not crushed by the rock that day. Can you solve this problem, like nocriz did?
Input
The first line contains an integer $T (1 \le T \le 10000)$ - the number of test cases. Then $T$ test cases follow.
The only line of each test case contains six integers $a,b,c,d,e,f(1 \le a,c \le 100, -100 \le e \le 100, $ $1 \le b,d \le 4\times 10^6, 0 \le f \le 10^{15})$.
It is guaranteed that there are no more than $1000$ test cases for which $\max_{(x,y) \in E} \max(x,y)>100$; no more than $100$ test cases for which $\max_{(x,y) \in E} \max(x,y)>1000$; no more than $10$ test cases for which $\max_{(x,y) \in E} \max(x,y)>10000$; no more than $3$ test cases for which $\max_{(x,y) \in E} \max(x,y)>1000000$; no more than $1$ test case for which $\max_{(x,y) \in E} \max(x,y)>2000000$, and $\sum \max_{(x,y) \in E} \max(x,y) \leq 1.1 \times 10^7$.
The only line of each test case contains six integers $a,b,c,d,e,f(1 \le a,c \le 100, -100 \le e \le 100, $ $1 \le b,d \le 4\times 10^6, 0 \le f \le 10^{15})$.
It is guaranteed that there are no more than $1000$ test cases for which $\max_{(x,y) \in E} \max(x,y)>100$; no more than $100$ test cases for which $\max_{(x,y) \in E} \max(x,y)>1000$; no more than $10$ test cases for which $\max_{(x,y) \in E} \max(x,y)>10000$; no more than $3$ test cases for which $\max_{(x,y) \in E} \max(x,y)>1000000$; no more than $1$ test case for which $\max_{(x,y) \in E} \max(x,y)>2000000$, and $\sum \max_{(x,y) \in E} \max(x,y) \leq 1.1 \times 10^7$.
Output
For each test case, output one integer representing the answer.
Sample Input
2 2 2 1 3 -1 6 13 19 11 17 6 1919
Sample Output
483333436 102810867
Hint
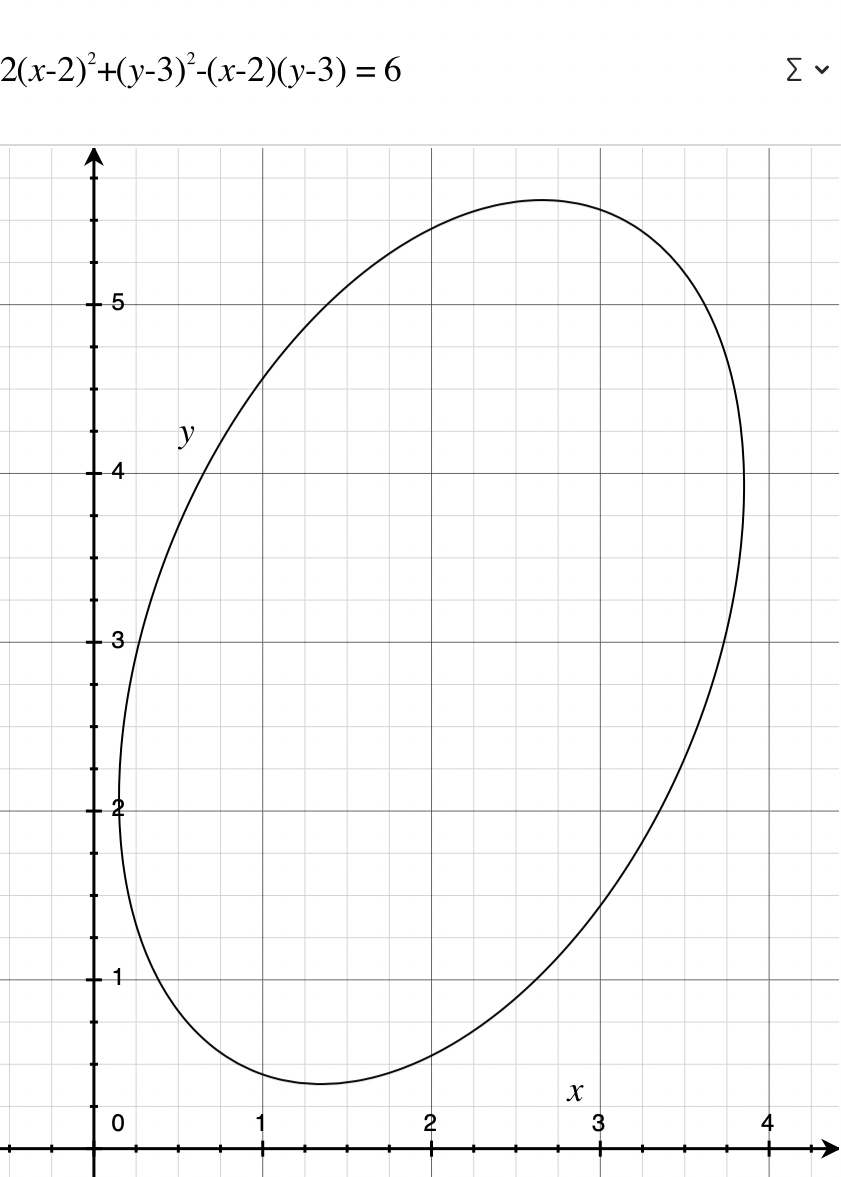
Source
| Home | Top |
Hangzhou Dianzi University Online Judge 3.0 Copyright © 2005-2025 HDU ACM Team. All Rights Reserved. Designer & Developer : Wang Rongtao LinLe GaoJie GanLu Total 0.000000(s) query 1, Server time : 2025-04-01 07:25:42, Gzip enabled |
Administration |