VC Is All You Need

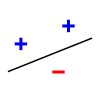
Three points example.



Four points example.

In this picture you can draw a line to seperate these $3$ points in the two dimensional plane to keep points with the same color lie in the same side no matter how to color each point using either blue or red.

But in $k$ dimensional real Euclidean space $R^k$, can you find $n$ points satisfying that there always exsit a $k-1$ dimensional hyperplane to seperate them in any one of $2^n$ coloring schemes?

The first line contains only one integer $T(1 \le T \le 10^5)$ denoting the number of test cases.

Each of next $T$ lines contains two integers $n, k \in [2,10^{18}]$ seperated by a space.

Print $Yes$ if you can find one solution, or print $No$ if you cannot.

3
2 2
3 2
4 2

Yes
Yes
No

2021“MINIEYE杯”中国大学生算法设计超级联赛（5）