
| Online Judge | Online Exercise | Online Teaching | Online Contests | Exercise Author |
|
F.A.Q Hand In Hand Online Acmers |
Best Coder beta VIP | STD Contests DIY | Web-DIY beta |
PE Class
Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 262144/262144 K (Java/Others)Total Submission(s): 110 Accepted Submission(s): 33
Special Judge
Problem Description
This class is on PE. Today, Baby Volcano is going to take part in a running competition in a maze. Could you help him win this competition?
For simplicity, we assume that this maze lies in a Euclidean plane. There is a graphical description for the maze shown in the following figure. We give some explanation here:
1. There are two kinds of obstructions in this maze, walls and doors. In the figure, black segments and rays are walls, red segments are doors. Some doors are closed while others are open. Baby volcano couldn't go through walls and closed doors, while he could pass open doors. He couldn't tell whether a door is open or not before reaching $its\ midpoint$.
2. In the outmost layer there are $5$ pieces of walls, corresponding to segment $GE,EF,FH$, and ray $GI,HJ$.
3. In the inner part there are $n$ layers of obstructions, the obstructions in the $i$-layer lies in $y=i$, consists of $i$ doors and $i-1$ walls, every obstruction is a segment with length $1$. The $j$-th door$(1\leq j \leq i)$ in $i$-th layer is the segement $\left(\left(\frac{1-2i}{2}+2j-2,i\right),\left(\frac{1-2i}{2}+2j-1,i\right)\right)$. The $j$-th wall$(1\leq j \leq i-1)$ in $i$-th layer is the segement
$\left(\left(\frac{1-2i}{2}+2j-1,i\right),\left(\frac{1-2i}{2}+2j,i\right)\right)$
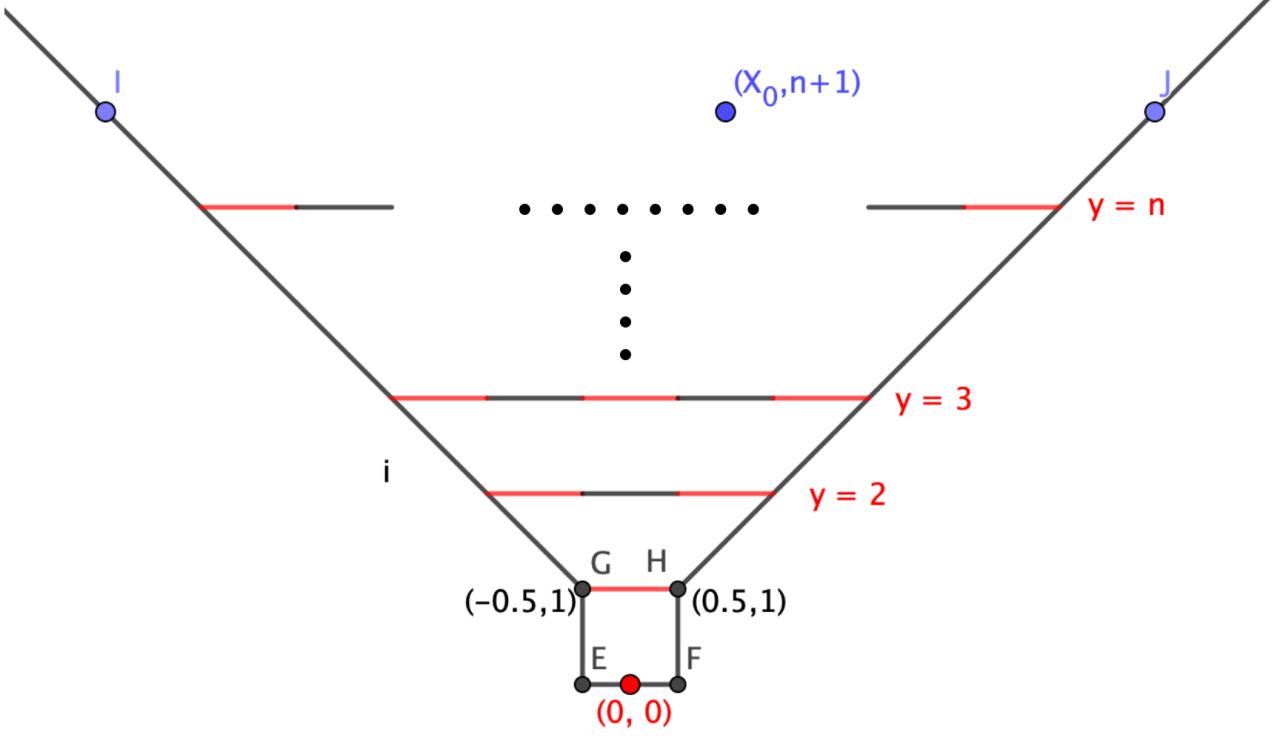
Now for every $1\leq i\leq n$, the teacher uniformly randomly choose $k_i$($1\leq k_i\leq i$) doors to be open. Baby Volcano wonders, if he starts at $(x_0,n+1)$, and try to approach $(0,0)$, what is the minimum expected length of walk?
For simplicity, we assume that this maze lies in a Euclidean plane. There is a graphical description for the maze shown in the following figure. We give some explanation here:
1. There are two kinds of obstructions in this maze, walls and doors. In the figure, black segments and rays are walls, red segments are doors. Some doors are closed while others are open. Baby volcano couldn't go through walls and closed doors, while he could pass open doors. He couldn't tell whether a door is open or not before reaching $its\ midpoint$.
2. In the outmost layer there are $5$ pieces of walls, corresponding to segment $GE,EF,FH$, and ray $GI,HJ$.
3. In the inner part there are $n$ layers of obstructions, the obstructions in the $i$-layer lies in $y=i$, consists of $i$ doors and $i-1$ walls, every obstruction is a segment with length $1$. The $j$-th door$(1\leq j \leq i)$ in $i$-th layer is the segement $\left(\left(\frac{1-2i}{2}+2j-2,i\right),\left(\frac{1-2i}{2}+2j-1,i\right)\right)$. The $j$-th wall$(1\leq j \leq i-1)$ in $i$-th layer is the segement
$\left(\left(\frac{1-2i}{2}+2j-1,i\right),\left(\frac{1-2i}{2}+2j,i\right)\right)$

Now for every $1\leq i\leq n$, the teacher uniformly randomly choose $k_i$($1\leq k_i\leq i$) doors to be open. Baby Volcano wonders, if he starts at $(x_0,n+1)$, and try to approach $(0,0)$, what is the minimum expected length of walk?
Input
In the first line there is a number $T$, denotes the number of test cases.
Next, there are $2\times T$ lines demonstrating each test case.
For every case, in the first line there are two integers, $n,x_0$, denotes the number of layers in this maze and the start position of Baby Volcano.
In the second line there are $n$ integers $k_1,k_2,k_3,\cdots,k_n$, showing the number of doors open in the $i$-th layer.
The input guarantees that $1 \leq T \leq 100,1 \leq n \leq 50$, and $-n\leq x_0\leq n$.
Next, there are $2\times T$ lines demonstrating each test case.
For every case, in the first line there are two integers, $n,x_0$, denotes the number of layers in this maze and the start position of Baby Volcano.
In the second line there are $n$ integers $k_1,k_2,k_3,\cdots,k_n$, showing the number of doors open in the $i$-th layer.
The input guarantees that $1 \leq T \leq 100,1 \leq n \leq 50$, and $-n\leq x_0\leq n$.
Output
Output $T$ real numbers, for each test case, you need to output $d$, denotes the minimum expected length of walk. You need to output six decimal places.
Sample Input
4 2 1 1 2 2 1 1 1 3 2 1 2 3 4 2 1 2 2 1
Sample Output
3.414213 4.414213 4.828427 10.323520
Source
| Home | Top |
Hangzhou Dianzi University Online Judge 3.0 Copyright © 2005-2024 HDU ACM Team. All Rights Reserved. Designer & Developer : Wang Rongtao LinLe GaoJie GanLu Total 0.000000(s) query 1, Server time : 2024-11-22 16:01:28, Gzip enabled |
Administration |