Coin Game

There are $n$ machines in front of you, and each of them has a cute button on it.

For the $i$-th machine, if you push the button on it, it will give you a coin valued at $a_i$. If you push the button again, it will give you a coin valued at $b_i$. If you push the button the third time, it will give you a coin valued at $a_i$ again. However, it won't give you coins any more even you push the button because the $i$-th machine only has three coins.

Now you want to obtain $k$ coins from these machines, and you should make the total value of these coins as maximum as possible. Let's denote the maximum total value of these $k$ coins as $f(k)$.

You are required to output the value of $f(1) \oplus f(2) \oplus f(3) \oplus \cdots \oplus f(m)$, where $m$ is a given number and $\oplus$ means the xor operatation.

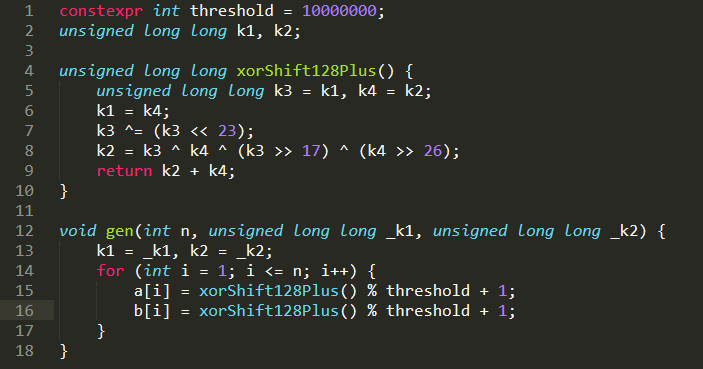
To avoid spending too much time reading all the data, we use xorshift128plus algorithm to generate the testdata, this algorithm is parameterized with two initial seed $k_1$ and $k_2$. Please refer to the code (written in C++) in the below:

There are multiple test cases,please read until the end of the file.

For each test case, it contains only four integer $n, m, k_1, k_2$. $1 \le n \le 5\times 10^6$, $1 \le m \le 1.5 \times 10^7$, $1 \le k_1, k_2 \le 10^{12}$ in one line.

Output the answer in one line for each test case.

2 6 123456789 987654321
10 20 19260817 71806291

6935157
41506271

2020 Multi-University Training Contest 10