
| Online Judge | Online Exercise | Online Teaching | Online Contests | Exercise Author |
|
F.A.Q Hand In Hand Online Acmers |
Best Coder beta VIP | STD Contests DIY | Web-DIY beta |
Jumping on a Cactus
Time Limit: 2000/2000 MS (Java/Others) Memory Limit: 524288/524288 K (Java/Others)Total Submission(s): 77 Accepted Submission(s): 31
Problem Description
It is preferrable to read the pdf statment.
Cuber QQ has recently learned jumping on graphs. He now wants to demonstrate his skills on a cactus.
Recall that, cactus refers to a graph with every edge appearing in at most one cycle. If you do not know what a cycle is, formally, a cycle of length $k$ denotes an edge sequence $(u_1,u_2), (u_2,u_3),\ldots,(u_{k-1},u_k),(u_k,u_1)$.
Assuming you are given an undirected cactus $G=(V, E)$, with $n$ vertices and $m$ edges. A jumping on the cactus can be thought of as a visit to all vertices where every vertex is visited exactly once. That can be represented with a permutation of $1$ to $n$, $p_1, p_2, \ldots, p_n$, and they are visited in order.
Cuber QQ also wishes his jumping to be gradually approaching or distancing away from a particular node $e$. Concretely, we define $d(a, b)$ to be the distance from $a$ to $b$ (the minimum edges needs to be passed through from $a$ to $b$). A jumping is defined to be monotonic if,
Count the number of different monotonic jumping plans. Since the answer can be very large, you should print the answer modulo $998~244~353$.
Cuber QQ has recently learned jumping on graphs. He now wants to demonstrate his skills on a cactus.
Recall that, cactus refers to a graph with every edge appearing in at most one cycle. If you do not know what a cycle is, formally, a cycle of length $k$ denotes an edge sequence $(u_1,u_2), (u_2,u_3),\ldots,(u_{k-1},u_k),(u_k,u_1)$.
Assuming you are given an undirected cactus $G=(V, E)$, with $n$ vertices and $m$ edges. A jumping on the cactus can be thought of as a visit to all vertices where every vertex is visited exactly once. That can be represented with a permutation of $1$ to $n$, $p_1, p_2, \ldots, p_n$, and they are visited in order.
Cuber QQ also wishes his jumping to be gradually approaching or distancing away from a particular node $e$. Concretely, we define $d(a, b)$ to be the distance from $a$ to $b$ (the minimum edges needs to be passed through from $a$ to $b$). A jumping is defined to be monotonic if,
- for all edges $(u, v) \in E$, $d(u, e) < d(v, e)$ when $u$ is visited before $v$, or,
- for all edges $(u, v) \in E$, $d(u, e) > d(v, e)$ when $u$ is visited after $v$.
Count the number of different monotonic jumping plans. Since the answer can be very large, you should print the answer modulo $998~244~353$.
Input
The first line of the input contains a single integer $T$ ($1\le T\le 30$), denoting the number of test cases.
For each of the next $T$ cases:
There are at most $10$ test cases where $n\ge 1~000$.
For each of the next $T$ cases:
- The first line contains three space-separated integers $n$, $m$, $e$ ($2\le n\le 5~000$, $1\le m\le 2(n-1)$, $1\le e\le n$).
- The $i$-th of the next $m$ lines contains two space-separated integers $u_i$, $v_i$ ($1\le u_i,v_i\le n$, $u_i\ne v_i$). It is guaranteed that $d(u_i, e) \ne d(v_i, e)$.
There are at most $10$ test cases where $n\ge 1~000$.
Output
For each test case, output one line contains one integer denoting the answer modulo $998~244~353$.
For the example, $G$ looks like:
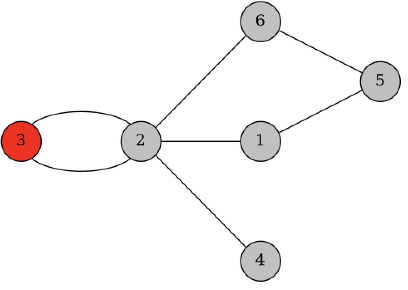
$3$ is the index of reference vertex.
There are $8$ correct permutations:
Notes
For the example, $G$ looks like:

$3$ is the index of reference vertex.
There are $8$ correct permutations:
- $\{ 3,2,4,1,6,5 \}$.
- $\{ 3,2,1,4,6,5 \}$.
- $\{ 3,2,1,6,4,5 \}$.
- $\{ 3,2,1,6,5,4 \}$.
- $\{ 3,2,4,6,1,5 \}$.
- $\{ 3,2,6,4,1,5 \}$.
- $\{ 3,2,6,1,4,5 \}$.
- $\{ 3,2,6,1,5,4 \}$.
Sample Input
1 6 7 3 6 2 5 6 1 5 1 2 3 2 3 2 4 2
Sample Output
8
Source
| Home | Top |
Hangzhou Dianzi University Online Judge 3.0 Copyright © 2005-2025 HDU ACM Team. All Rights Reserved. Designer & Developer : Wang Rongtao LinLe GaoJie GanLu Total 0.000000(s) query 1, Server time : 2025-03-31 07:32:04, Gzip enabled |
Administration |