Hexagon

It is preferrable to read the pdf statment.

If the world is a hexagon, I will take as many turns as possible before reaching the end.

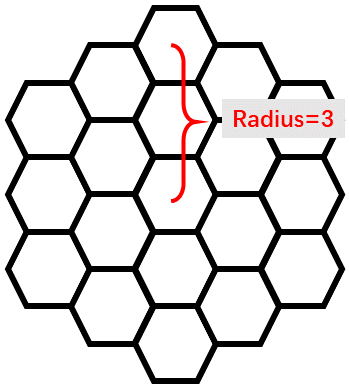
Cuber QQ has constructed a hexagon grid with radius $n$. This will be better if explained in a picture. For example, this is a hexagon grid with radius $3$:



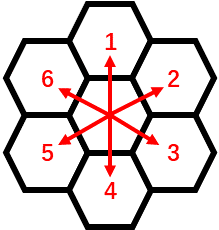
He challenges you take a perfect tour over the hexagon, that is to visit each cell exactly once. Starting from any point in the grid, you can move to any adjacent cell in each step. There are six different directions you can choose from:



Of course, if you are on the boundary, you cannot move outside of the hexagon.

Let $D(x,y)$ denote the direction from cell $x$ to $y$, and sequence $A$ denotes your route, in which $A_i$ denotes the $i$-th cell you visit. For index $i$ ($1 < i < |A|$), if $D(A_{i-1},A_i) \ne D(A_i,A_{i+1})$, we say there is a turning on cell $i$.

Maximize the number of turning while ensuring that each cell is visited exactly once. Print your route. If there are multiple solution, print any.

The first line of the input contains a single integer $T$ ($1\le T\le 10^4$), denoting the number of test cases.

Each of the next $T$ cases:

The first line contains an integer $n$ ($2\le n\le 500$).

It is guaranteed that the sum of $n$ doesn't exceed $2 \cdot 10^4$.

For each test case, output one line contains a string with $3(n-1)n$ characters. The $i$-th character is $D(A_i,A_{i+1})$.

1
2

313456

2020 Multi-University Training Contest 8