
| Online Judge | Online Exercise | Online Teaching | Online Contests | Exercise Author |
|
F.A.Q Hand In Hand Online Acmers |
Best Coder beta VIP | STD Contests DIY | Web-DIY beta |
Domino Covering
Time Limit: 6000/6000 MS (Java/Others) Memory Limit: 524288/524288 K (Java/Others)Total Submission(s): 24 Accepted Submission(s): 2
Problem Description
Elizur has an empty $n \times m$ grid and he wants to use some $1 \times 2$ and $2 \times 1$ dominoes to cover the entire grid. In the grid, each domino ought to cover exactly two adjacent squares and each square ought to be covered by exactly one domino, where two squares are adjacent if and only if they share a common side.
Obviously, he can achieve that if and only if at least one of $n$ and $m$ is even. In case that both $n$ and $m$ are odd, there is always a square that must be left empty. Hence, he intends to know in how many ways he can cover the entire grid. Two ways are considered different if and only if there exist two dominoes, each selected from one way, satisfying that they cover exactly one square at the same position.
Can you help him determine the answer? The answer may be exceedingly large, so he only requests you to tell him the answer modulo a prime number $p$.
Obviously, he can achieve that if and only if at least one of $n$ and $m$ is even. In case that both $n$ and $m$ are odd, there is always a square that must be left empty. Hence, he intends to know in how many ways he can cover the entire grid. Two ways are considered different if and only if there exist two dominoes, each selected from one way, satisfying that they cover exactly one square at the same position.
Can you help him determine the answer? The answer may be exceedingly large, so he only requests you to tell him the answer modulo a prime number $p$.
Input
The first line contains a single integer $T~(1 \leq T \leq 20\,000)$, indicating the number of questions.
In the next $T$ lines, each line contains three integers $n~(1 \leq n \leq 35)$, $m~(1 \leq m \leq 10^{18})$ and $p~(2 \leq p \leq 2^{30})$, representing a question he wants to ask you.
It is guaranteed that no more than $1\,000$ cases satisfy $n > 5$ or $m > 10^9$.
In the next $T$ lines, each line contains three integers $n~(1 \leq n \leq 35)$, $m~(1 \leq m \leq 10^{18})$ and $p~(2 \leq p \leq 2^{30})$, representing a question he wants to ask you.
It is guaranteed that no more than $1\,000$ cases satisfy $n > 5$ or $m > 10^9$.
Output
For each question, output a single integer in one line, denoting the answer modulo $p$.
Sample Input
6 2 2 23 2 3 233 3 3 2333 3 4 23333 4 4 2332333 5 251346744251346744 998244353
Sample Output
2 3 0 11 36 295381485
Hint
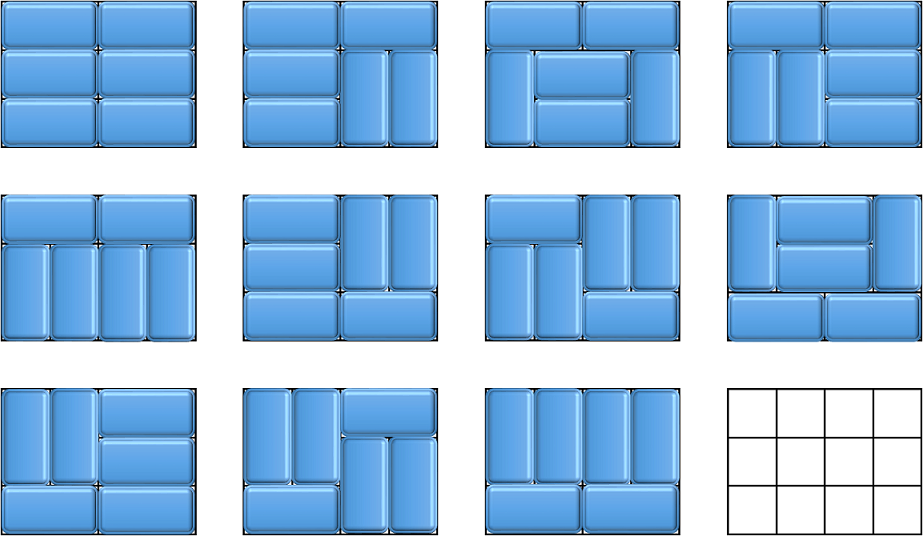
The following image shows all possible ways (11 in total) for the 3×4 grid.
Source
| Home | Top |
Hangzhou Dianzi University Online Judge 3.0 Copyright © 2005-2025 HDU ACM Team. All Rights Reserved. Designer & Developer : Wang Rongtao LinLe GaoJie GanLu Total 0.000000(s) query 1, Server time : 2025-04-01 10:04:07, Gzip enabled |
Administration |