Line Graphs

Last year, Rounddog participated in a contest with a pretty hard problem set and failed in solving the problem about line graphs. So he decides to make a deep study of line graphs these days.

In the mathematical discipline of graph theory, the line graph of a simple undirected graph $G$ is another simple undirected graph $L(G)$ that represents the adjacency between every two edges in $G$.
Precisely speaking, for an undirected graph $G$ without loops or multiple edges, its line graph $L(G)$ is a graph such that
- each vertex of $L(G)$ represents an edge of $G$; and
- two vertices of $L(G)$ are adjacent if and only if their corresponding edges share a common endpoint in $G$.



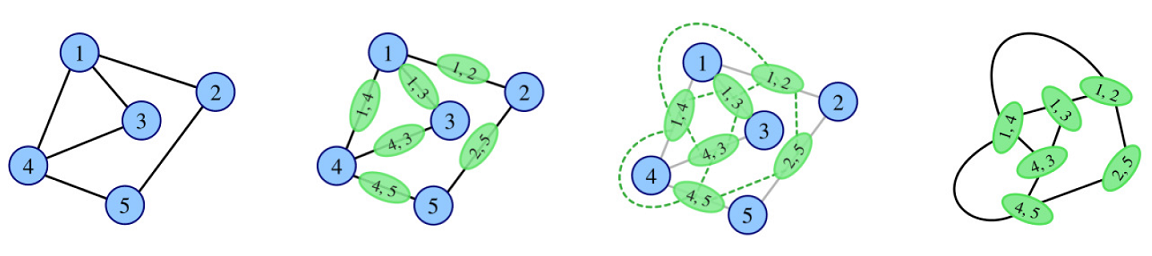
Given a simple undirected graph $G$, Rounddog's study aims to find the maximum cliques in its line graph $L(G)$ and he decides to make some critical results of his early study as a challenge for you.

In this problem, you are given a simple undirected graph $G$ and a small positive integer $k$. After finding all maximum cliques in $L^k(G)$, where $L^0(G)=G$ and $L^s(G)=L(L^{s-1}(G))$ for each positive integer $s$, you need to show Rounddog the number of vertices in one of the maximum cliques and the number of distinct maximum cliques modulo $1\,000\,000\,007$.

Here a subset of vertices of an undirected graph is called clique if and only if there is an edge between each pair of vertices in the subset, and maximum cliques are those cliques with the maximum number of vertices.

The input contains several test cases, and the first line contains a single integer $T~(1 \le T \le 1\,000)$, the number of test cases.

For each test case, the first line contains three integers $n~(1 \le n \le 100\,000)$, $m~(0 \le m \le 200\,000)$ and $k~(1 \le k \le 4)$, the number of vertices and edges in the given simple undirected graph $G$ and the number of iterations of the line graph operation.

Then $m$ lines follow, describing all edges of the graph.
Each line of them contains two integers $u$ and $v~(1 \le u, v \le n, u \ne v)$, representing an edge between the $u$-th vertex and the $v$-th vertex.

It is guaranteed that the sum of $n$ in all test cases does not exceed $2\,000\,000$, the sum of $m$ does not exceed $3\,000\,000$, and the graph in each test case contains no loops or multiple edges.

For each test case, output a single line with two integers, the number of vertices in one of the maximum cliques and the number of distinct maximum cliques modulo $1\,000\,000\,007$.

3
5 0 4
5 4 1
1 2
1 3
1 4
1 5
5 4 4
1 2
1 3
1 4
1 5

0 1
4 1
6 12

2019 Multi-University Training Contest 10