Acesrc and Cube Hypernet

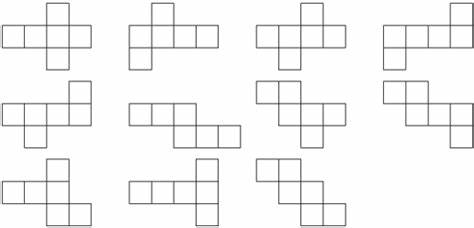
Acesrc is fond of cube nets. If we cut some edges of a cube, the surface of the cube can be unfolded into 2-dimensional space, and the resulting flat shape is called a cube net. There are 11 essentially different cube nets, listed below.



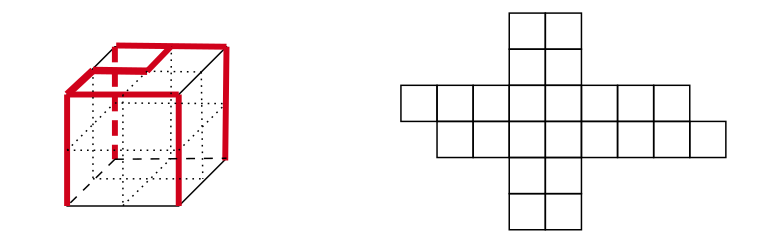
In this problem, we consider a generalization of the cube net, called cube hypernet. For each face of a cube, we divide it into $k \times k$ small square cells. If we cut some edges of these small cells, the surface of the cube can be unfolded into 2-dimensional space, then the resulting flat shape is a cube hypernet. Clearly, cube nets are just a special type of cube hypernets where $k = 1$. The following picture illustrates a cube hypernet and explains how it is formed.



Identifying cube nets is a relatively easy job; however, this might not be true for cube hypernets. Here comes the challenge. Given a flat shape composed of small squares, determine whether it is a cube hypernet.

The first line of the input is a single integer $T$ $(1 \leq T \leq 30)$, denoting the number of test cases.

For each test case, the first line contains two integers $h, w$ $(1 \leq h, w \leq 100)$, denoting the height and width of the input region. Each of the remaining $h$ lines contains $w$ characters, either $\texttt{'#'}$ or $\texttt{'.'}$. The character $\texttt{'#'}$ means that the square is part of the shape, while $\texttt{'.'}$ not.

It is guaranteed that the input shape is nonempty and connected in four directions, and there is no hole inside the shape, not even a hole 8-connected to the outside. Also, the sum of $h \times w$ over all test cases does not exceed 35000.

For each test case, output $\texttt{yes}$ in a line if the input shape is cube hypernet, and $\texttt{no}$ otherwise.

2
6 9
...##....
...##....
########.
.########
...##....
...##....
1 6
######

yes
no

2019 Multi-University Training Contest 8