Intersection of Prisms

Cuber QQ used to encounter such a problem: find the intersection of two infinitely long convex right prisms $A$ and $B$. Actually this problem is also on HDU Online Judge, you can solve it afterwards if you are interested.

Cuber QQ quickly solved it, and thought it too easy because his program can handle more than that. So he modify it a little bit, by removing the constraints of ``convex'', that is, the cross-section of these two prisms are not necessarily convex, but they are still simple.

Formally, you have to find the volume of intersection of two prisms, whose cross-sections are both simple polygons. All joining edges of $A$ are parallel to the $z$-axis, and all joining edges of $B$ are parallel to the $x$-axis. If A and B do not intersect, the answer is $0$ of course.

The first line is an integer $t$, denoting the number of test cases follows.

For each test case, there are two polygons, the base polygon of $A$ and $B$ respectively.

An integer $n$ ($3 \le n \le 10^5$) followed by $n$ lines, each containing two space-separated integers $(x, y)$ ($-10^6 \le x, y \le 10^6$), is the representation of the base polygon of $A$. The following $m+1$ ($3 \le m \le 10^5$) gives a similar representation for $B$, except that the coordinates given are $(y, z)$ ($-10^6 \le x, y \le 10^6$).

Each polygon are given in either clockwise or counterclockwise order. Following the convention, polygon $P$ is simple, if no two edges have any points in common, with the obvious exception of two consecutive segments having one common point.

The sum of $m+n$ from all test cases does not exceed $2 \cdot 10^6$.

For each test case, output the answer modulo $10^9+7$, that is, if the answer is $\frac{P}{Q}$, you should output $P \cdot Q^{-1}$ modulo $10^9+7$, where $Q^{-1}$ denotes the multiplicative inverse of $Q$ modulo $10^9+7$.

1
4
10 0
0 10
-10 0
0 -10
3
5 0
-15 -10
-15 10

666667713

The intersection of the sample input is 3125/3.

Prisms before intersection:




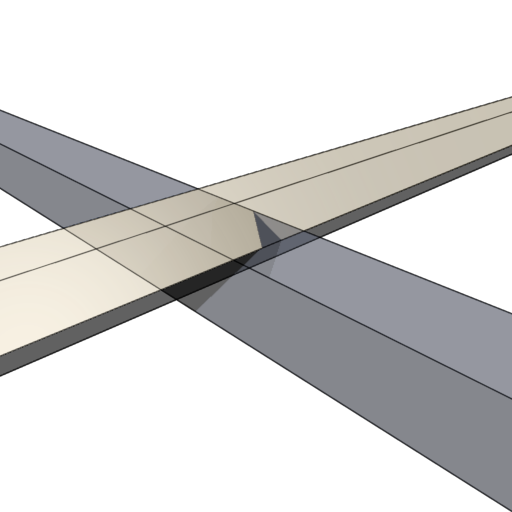
The intersection part looks like this:



The input size is quite large. Please mind the efficiency of your input buffer.

2019 Multi-University Training Contest 7