
| Online Judge | Online Exercise | Online Teaching | Online Contests | Exercise Author |
|
F.A.Q Hand In Hand Online Acmers |
Best Coder beta VIP | STD Contests DIY | Web-DIY beta |
Search for Answer
Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 65536/65536 K (Java/Others)Total Submission(s): 156 Accepted Submission(s): 57
Problem Description
Given a tournament, you need to determine the direction of the remaining sides to maximize the answer. The answer is calculated in the following way. The vertices are labeled from $0$ to $n-1$, and the matrix $s$ is used to represent the edges.
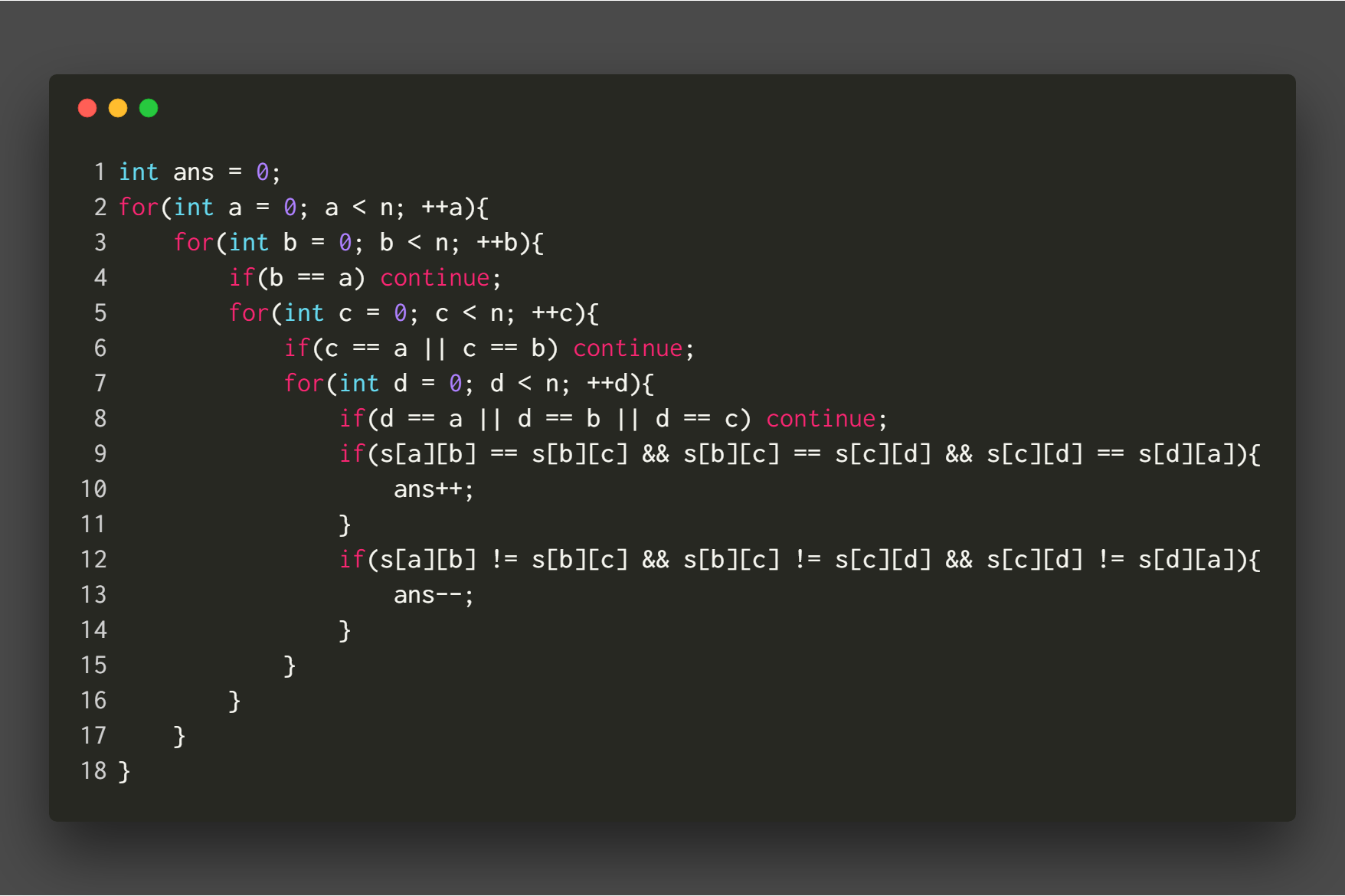

Input
The first line of input is a single line of integer $T (2 \le T \le 10)$, the number of test cases. In each test case, there are $1$ integers $n(5 \le n \le 200)$, denoting the number of vertices. Then in the following $n$ lines, the $i$-th line has a string of length $n$. If $s[i][j]=1$, there is an edge from $i$ to $j$. If $s[i][j]=2$ means you need to determine the direction for that edge. The input is guaranteed to be legal, and the number of $(i, j) (i < j)$ satisfying $s[i][j]=s[j][i]=2$ is less than $200$. The data is randomly generated.
Output
For each set of test samples, output one line to represent the maximized answer.
Sample Input
2 5 02112 20221 02001 02102 20020 5 01112 00022 01012 02002 22220
Sample Output
40 24
Hint
One solution to the first case is:
00110
10001
01001
01100
10010
Source
| Home | Top |
Hangzhou Dianzi University Online Judge 3.0 Copyright © 2005-2025 HDU ACM Team. All Rights Reserved. Designer & Developer : Wang Rongtao LinLe GaoJie GanLu Total 0.000000(s) query 1, Server time : 2025-03-29 10:14:39, Gzip enabled |
Administration |