
| Online Judge | Online Exercise | Online Teaching | Online Contests | Exercise Author |
|
F.A.Q Hand In Hand Online Acmers |
Best Coder beta VIP | STD Contests DIY | Web-DIY beta |
Rikka with Treasure
Time Limit: 20000/10000 MS (Java/Others) Memory Limit: 524288/524288 K (Java/Others)Total Submission(s): 58 Accepted Submission(s): 15
Problem Description
By coincidentally, Rikka found a treasure map. She wants to employ several expedition teams to help her find the treasure.
There are $n$ caves in the treasure maps and $n-1$ undirected roads between the caves. For each cave pair $(i,j)(i \neq j)$, it is guaranteed that there is exactly one simple path between them, and the distance $d(i,j)$ between these two caves is defined by the number of caves in this path.
For example, in the following treasure map, $d(1,3) = 3, d(2, 5) = 2$ and $d(1,4)=4$.
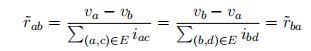
Some of the caves have depots near them. Each expedition team can explore all the caves on the path ($s_i$, $t_i$)($s_i$ may be equal to $t_i$) which satisfies there are depots near $s_i$, $t_i$, and $s_i,t_i$ are stipulated by Rikka. After the exploration, Rikka needs to pay $d(s_i,t_i) \times C$ dollars to this team.
Each cave has treasure in it and the treasure in the $i$th cave worths $a_i$ dollars. Rikka can get $i$th treasure if and only if there are at least one expedition teams which have explored $i$th cave.
For example, in the previous treasure map, if $a_i=i,C=1$, all caves have depots near them, Rikka employs two expedition teams and the first team explores path $(1,5)$, the second team explores $(2,3)$, then Rikka need pay $3$ dollars to the first team, $2$ dollars to the second team, and Rikka can get treasure $1,2,3,5$. So the Rikka's income will be $1+2+3+5-3-2=6$ dollars.
Now, for each $K$ from $1$ to $n$, Rikka wants to calculate the maximum possible income she can get if she employs at most $K$ expedition teams.
There are $n$ caves in the treasure maps and $n-1$ undirected roads between the caves. For each cave pair $(i,j)(i \neq j)$, it is guaranteed that there is exactly one simple path between them, and the distance $d(i,j)$ between these two caves is defined by the number of caves in this path.
For example, in the following treasure map, $d(1,3) = 3, d(2, 5) = 2$ and $d(1,4)=4$.
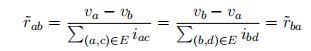
Some of the caves have depots near them. Each expedition team can explore all the caves on the path ($s_i$, $t_i$)($s_i$ may be equal to $t_i$) which satisfies there are depots near $s_i$, $t_i$, and $s_i,t_i$ are stipulated by Rikka. After the exploration, Rikka needs to pay $d(s_i,t_i) \times C$ dollars to this team.
Each cave has treasure in it and the treasure in the $i$th cave worths $a_i$ dollars. Rikka can get $i$th treasure if and only if there are at least one expedition teams which have explored $i$th cave.
For example, in the previous treasure map, if $a_i=i,C=1$, all caves have depots near them, Rikka employs two expedition teams and the first team explores path $(1,5)$, the second team explores $(2,3)$, then Rikka need pay $3$ dollars to the first team, $2$ dollars to the second team, and Rikka can get treasure $1,2,3,5$. So the Rikka's income will be $1+2+3+5-3-2=6$ dollars.
Now, for each $K$ from $1$ to $n$, Rikka wants to calculate the maximum possible income she can get if she employs at most $K$ expedition teams.
Input
The first line contains a single integer $t(1 \leq t \leq 10^3)$, the number of the testcases.
For each testcase, the first line contains three integers $n,C(1 \leq n \leq 3000, 1 \leq C \leq 10^7)$.
The second line contains $n$ 01 integers $p_i$. $p_i=1$ if and only if there is a depot near the $i$th cave.
The third line contains $n$ integers $a_i(1 \leq a_i \leq 10^7)$, which describes the value of the treasure.
Then $n-1$ lines follow, each line contains two integers $u_i,v_i$, which describes one road in the map.
The input guarantees that there are at least one depots and there are at most $5$ testcases with $n > 200$.
For each testcase, the first line contains three integers $n,C(1 \leq n \leq 3000, 1 \leq C \leq 10^7)$.
The second line contains $n$ 01 integers $p_i$. $p_i=1$ if and only if there is a depot near the $i$th cave.
The third line contains $n$ integers $a_i(1 \leq a_i \leq 10^7)$, which describes the value of the treasure.
Then $n-1$ lines follow, each line contains two integers $u_i,v_i$, which describes one road in the map.
The input guarantees that there are at least one depots and there are at most $5$ testcases with $n > 200$.
Output
For each testcase, output a single line with a $n$ integers, the maximum possible income Rikka can get if she employs at most $i$ expedition teams.
Sample Input
5 5 1 1 0 1 0 1 1 2 3 4 5 1 2 2 3 2 5 3 4 5 1 1 0 1 1 1 1 2 3 4 5 1 2 2 3 2 5 3 4 5 1 1 1 1 1 1 1 2 3 4 5 1 2 2 3 2 5 3 4 5 2 1 0 1 0 1 1 2 3 4 5 1 2 2 3 2 5 3 4 5 1 1 1 1 1 1 1 2 3 4 5 1 2 1 3 1 4 1 5
Sample Output
7 7 7 7 7 10 10 10 10 10 10 10 10 10 10 4 4 4 4 4 7 9 10 10 10
Source
| Home | Top |
Hangzhou Dianzi University Online Judge 3.0 Copyright © 2005-2024 HDU ACM Team. All Rights Reserved. Designer & Developer : Wang Rongtao LinLe GaoJie GanLu Total 0.000000(s) query 1, Server time : 2024-11-22 10:21:19, Gzip enabled |
Administration |