
| Online Judge | Online Exercise | Online Teaching | Online Contests | Exercise Author |
|
F.A.Q Hand In Hand Online Acmers |
Best Coder beta VIP | STD Contests DIY | Web-DIY beta |
Pizza Hub
Time Limit: 3000/3000 MS (Java/Others) Memory Limit: 131072/131072 K (Java/Others)Total Submission(s): 1582 Accepted Submission(s): 302
Special Judge
Problem Description
Coffee Chicken has started a new restaurant named Pizza Hu...b! It provides various styles of pizzas, hamburgers, sandwiches, coffee, chickens and many other awesome Western cuisines. Welcome to Pizza Hub after this Multi-University Training Contest!
Since the pizzas are so exquisite, it is never a bad thing to design nice paper pads for them. The pizzas provided in Pizza Hub are sliced into triangles. The rectangular-shaped paper pads are cut from a paper strip of fixed width which is long enough. The pizza should be placed entirely on the pad; however, their borders are allowed to touch. Also, you are allowed to rotate the pizza.
As the customized paper strip is rather expensive, minimizing the size of the pizza pad can save a lot of money. Can you determine the minimum possible height of the pizza pad, given the width of the paper strip? The following picture illustrates the first sample test case.
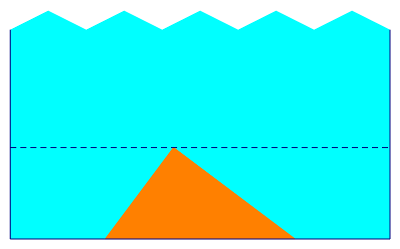
Since the pizzas are so exquisite, it is never a bad thing to design nice paper pads for them. The pizzas provided in Pizza Hub are sliced into triangles. The rectangular-shaped paper pads are cut from a paper strip of fixed width which is long enough. The pizza should be placed entirely on the pad; however, their borders are allowed to touch. Also, you are allowed to rotate the pizza.
As the customized paper strip is rather expensive, minimizing the size of the pizza pad can save a lot of money. Can you determine the minimum possible height of the pizza pad, given the width of the paper strip? The following picture illustrates the first sample test case.

Input
The first line of the input is a single integer $T$ $(1 \leq T \leq 50000)$, the number of test cases.
Each test case is a single line of seven integers $x_1, y_1, x_2, y_2, x_3, y_3$ $(0 \leq x_1, y_1, x_2, y_2, x_3, y_3 \leq 10000)$ and $w$ $(1 \leq w \leq 10000)$, where $(x_1, y_1)$, $(x_2, y_2)$ and $(x_3, y_3)$ are Cartesian coordinates of the vertices of the pizza, and $w$ is the width of the strip. It is guaranteed that the three vertices are not collinear.
Each test case is a single line of seven integers $x_1, y_1, x_2, y_2, x_3, y_3$ $(0 \leq x_1, y_1, x_2, y_2, x_3, y_3 \leq 10000)$ and $w$ $(1 \leq w \leq 10000)$, where $(x_1, y_1)$, $(x_2, y_2)$ and $(x_3, y_3)$ are Cartesian coordinates of the vertices of the pizza, and $w$ is the width of the strip. It is guaranteed that the three vertices are not collinear.
Output
For each test case, display the minimum height of the pizza pad with an absolute or relative error of no more than $10^{-6}$. If it is impossible to make a pizza pad, display $\texttt{impossible}$ instead.
Sample Input
2 0 0 3 0 0 4 10 0 0 3 0 0 4 1
Sample Output
2.400000000 impossible
Source
| Home | Top |
Hangzhou Dianzi University Online Judge 3.0 Copyright © 2005-2024 HDU ACM Team. All Rights Reserved. Designer & Developer : Wang Rongtao LinLe GaoJie GanLu Total 0.000000(s) query 1, Server time : 2024-11-22 09:30:26, Gzip enabled |
Administration |