
| Online Judge | Online Exercise | Online Teaching | Online Contests | Exercise Author |
|
F.A.Q Hand In Hand Online Acmers |
Best Coder beta VIP | STD Contests DIY | Web-DIY beta |
Everything Has Changed
Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 262144/262144 K (Java/Others)Total Submission(s): 1953 Accepted Submission(s): 982
Special Judge
Problem Description
Edward is a worker for Aluminum Cyclic Machinery. His work is operating mechanical arms to cut out designed models. Here is a brief introduction of his work.
Assume the operating plane as a two-dimensional coordinate system. At first, there is a disc with center coordinates $(0, 0)$ and radius $R$. Then, $m$ mechanical arms will cut and erase everything within its area of influence simultaneously, the $i$-th area of which is a circle with center coordinates $(x_i, y_i)$ and radius $r_i$ $(i = 1, 2, \cdots, m)$. In order to obtain considerable models, it is guaranteed that every two cutting areas have no intersection and no cutting area contains the whole disc.
Your task is to determine the perimeter of the remaining area of the disc excluding internal perimeter.
Here is an illustration of the sample, in which the red curve is counted but the green curve is not.
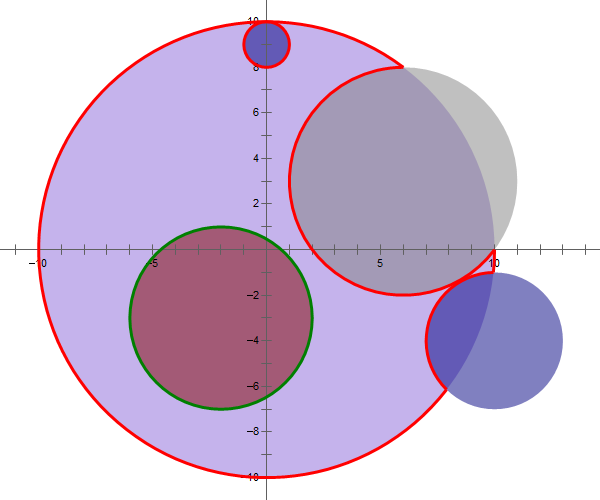
Assume the operating plane as a two-dimensional coordinate system. At first, there is a disc with center coordinates $(0, 0)$ and radius $R$. Then, $m$ mechanical arms will cut and erase everything within its area of influence simultaneously, the $i$-th area of which is a circle with center coordinates $(x_i, y_i)$ and radius $r_i$ $(i = 1, 2, \cdots, m)$. In order to obtain considerable models, it is guaranteed that every two cutting areas have no intersection and no cutting area contains the whole disc.
Your task is to determine the perimeter of the remaining area of the disc excluding internal perimeter.
Here is an illustration of the sample, in which the red curve is counted but the green curve is not.

Input
The first line contains one integer $T$, indicating the number of test cases.
The following lines describe all the test cases. For each test case:
The first line contains two integers $m$ and $R$.
The $i$-th line of the following $m$ lines contains three integers $x_i, y_i$ and $r_i$, indicating a cutting area.
$1 \leq T \leq 1000$, $1 \leq m \leq 100$, $-1000 \leq x_i, y_i \leq 1000$, $1 \leq R, r_i \leq 1000$ $(i = 1, 2, \cdots, m)$.
The following lines describe all the test cases. For each test case:
The first line contains two integers $m$ and $R$.
The $i$-th line of the following $m$ lines contains three integers $x_i, y_i$ and $r_i$, indicating a cutting area.
$1 \leq T \leq 1000$, $1 \leq m \leq 100$, $-1000 \leq x_i, y_i \leq 1000$, $1 \leq R, r_i \leq 1000$ $(i = 1, 2, \cdots, m)$.
Output
For each test case, print the perimeter of the remaining area in one line. Your answer is considered correct if its absolute or relative error does not exceed $10^{-6}$.
Formally, let your answer be $a$ and the jury's answer be $b$. Your answer is considered correct if $\frac{|a - b|}{\max(1, |b|)} \leq 10^{-6}$.
Formally, let your answer be $a$ and the jury's answer be $b$. Your answer is considered correct if $\frac{|a - b|}{\max(1, |b|)} \leq 10^{-6}$.
Sample Input
1 4 10 6 3 5 10 -4 3 -2 -4 4 0 9 1
Sample Output
81.62198908430238475376
Source
| Home | Top |
Hangzhou Dianzi University Online Judge 3.0 Copyright © 2005-2025 HDU ACM Team. All Rights Reserved. Designer & Developer : Wang Rongtao LinLe GaoJie GanLu Total 0.000000(s) query 1, Server time : 2025-03-29 21:13:11, Gzip enabled |
Administration |