Matching In Multiplication

In the mathematical discipline of graph theory, a bipartite graph is a graph whose vertices can be divided into two disjoint sets $U$ and $V$ (that is, $U$ and $V$ are each independent sets) such that every edge connects a vertex in $U$ to one in $V$. Vertex sets $U$ and $V$ are usually called the parts of the graph. Equivalently, a bipartite graph is a graph that does not contain any odd-length cycles. A matching in a graph is a set of edges without common vertices. A perfect matching is a matching that each vertice is covered by an edge in the set.



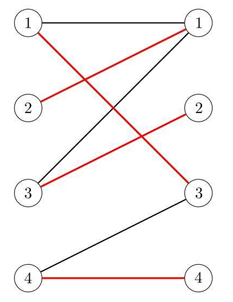
Little Q misunderstands the definition of bipartite graph, he thinks the size of $U$ is equal to the size of $V$, and for each vertex $p$ in $U$, there are exactly two edges from $p$. Based on such weighted graph, he defines the weight of a perfect matching as the product of all the edges' weight, and the weight of a graph is the sum of all the perfect matchings' weight.

Please write a program to compute the weight of a weighted ''bipartite graph'' made by Little Q.

The first line of the input contains an integer $T(1\leq T\leq15)$, denoting the number of test cases.

In each test case, there is an integer $n(1\leq n\leq 300000)$ in the first line, denoting the size of $U$. The vertex in $U$ and $V$ are labeled by $1,2,...,n$.

For the next $n$ lines, each line contains $4$ integers $v_{i,1},w_{i,1},v_{i,2},w_{i,2}(1\leq v_{i,j}\leq n,1\leq w_{i,j}\leq 10^9)$, denoting there is an edge between $U_i$ and $V_{v_{i,1}}$, weighted $w_{i,1}$, and there is another edge between $U_i$ and $V_{v_{i,2}}$, weighted $w_{i,2}$.

It is guaranteed that each graph has at least one perfect matchings, and there are at most one edge between every pair of vertex.

For each test case, print a single line containing an integer, denoting the weight of the given graph. Since the answer may be very large, please print the answer modulo $998244353$.

1
2
2 1 1 4
1 4 2 3

16

2017 Multi-University Training Contest - Team 4