
| Online Judge | Online Exercise | Online Teaching | Online Contests | Exercise Author |
|
F.A.Q Hand In Hand Online Acmers |
Best Coder beta VIP | STD Contests DIY | Web-DIY beta |
平行四边形
Time Limit: 4000/2000 MS (Java/Others) Memory Limit: 65536/65536 K (Java/Others)Total Submission(s): 674 Accepted Submission(s): 204
Problem Description
假设直线L和L'相交于原点O。假设S ={$ s_1, s_2,...,s_n$}是平面上的n个点。你打 算找四个点满足如下条件:
1. A $\in$ L 而 A' $\in$ L'。
2. B,B'都属于S;即 B$\in$S 且B'$\in$S。
3. A,A'的中点与B,B'的中点重叠。这意味着ABA'B'是一个平行四边形(或者退 化的平行四边形)。
4. 平行四边形ABA'B'的面积最大。
1. A $\in$ L 而 A' $\in$ L'。
2. B,B'都属于S;即 B$\in$S 且B'$\in$S。
3. A,A'的中点与B,B'的中点重叠。这意味着ABA'B'是一个平行四边形(或者退 化的平行四边形)。
4. 平行四边形ABA'B'的面积最大。
Input
包含多组测试数据。
第一行有4个整数a, b, a', b',分别描述L和L'的坐标方程。具体来说,L的方程 为 ax + by = 0 ;而 L'的方程为 a'x + b'y = 0。
第二行有一个整数n。
接下来n行每行两个整数,表示一对坐标,描述S中的n个点。
保证n <= $10^6$,其他输入整数的绝对值不超过$10^4$;保证ab'$\neq$ba',$a^2+ b^2>0, a'^2 + b'^2 > 0$。
第一行有4个整数a, b, a', b',分别描述L和L'的坐标方程。具体来说,L的方程 为 ax + by = 0 ;而 L'的方程为 a'x + b'y = 0。
第二行有一个整数n。
接下来n行每行两个整数,表示一对坐标,描述S中的n个点。
保证n <= $10^6$,其他输入整数的绝对值不超过$10^4$;保证ab'$\neq$ba',$a^2+ b^2>0, a'^2 + b'^2 > 0$。
Output
输出一个整数,表示最大平行四边形的面积四舍五入到整数的值。
保证所有数据中,最大面积在四舍五入前的小数部分在[0,0.4] $\bigcup$ [0.6,1)中。
保证所有数据中,最大面积在四舍五入前的小数部分在[0,0.4] $\bigcup$ [0.6,1)中。
Sample Input
1 0 0 1 5 1 1 -1 1 -1 -1 1 -1 0 0
Sample Output
2
Hint
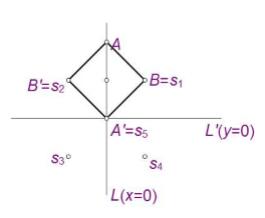
Source
| Home | Top |
Hangzhou Dianzi University Online Judge 3.0 Copyright © 2005-2025 HDU ACM Team. All Rights Reserved. Designer & Developer : Wang Rongtao LinLe GaoJie GanLu Total 0.000000(s) query 1, Server time : 2025-04-01 08:55:50, Gzip enabled |
Administration |