Auxiliary Set

Given a rooted tree with n vertices, some of the vertices are important.

An auxiliary set is a set containing vertices satisfying at least one of the two conditions：

$\bullet $It is an important vertex
$\bullet $It is the least common ancestor of two different important vertices.

You are given a tree with n vertices (1 is the root) and q queries.

Each query is a set of nodes which indicates the unimportant vertices in the tree. Answer the size (i.e. number of vertices) of the auxiliary set for each query.

The first line contains only one integer T ($T \leq 1000$), which indicates the number of test cases.

For each test case, the first line contains two integers n ($1 \leq n \leq 100000$), q ($0 \leq q \leq 100000$).

In the following n -1 lines, the i-th line contains two integers $u_i,v_i (1\leq u_i,v_i \leq n)$ indicating there is an edge between $u_i$i and $v_i$ in the tree.

In the next q lines, the i-th line first comes with an integer $m_i (1 \leq m_i \leq 100000)$ indicating the number of vertices in the query set.Then comes with mi different integers, indicating the nodes in the query set.

It is guaranteed that $\sum^q_{i=1} m_i \leq 100000$.

It is also guaranteed that the number of test cases in which $n \geq 1000$  or $\sum_{i=1}^{q} m_i \geq 1000$ is no more than 10.

For each test case, first output one line "Case #x:", where x is the case number (starting from 1).

Then q lines follow, i-th line contains an integer indicating the size of the auxiliary set for each query.

1
6 3
6 4
2 5
5 4
1 5
5 3
3 1 2 3
1 5
3 3 1 4

Case #1:
3
6
3

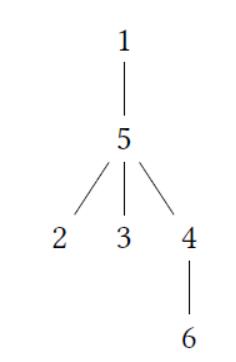
For the query {1，2, 3}:
•node 4, 5, 6 are important nodes For the query {5}：
•node 1，2, 3, 4, 6 are important nodes
•node 5 is the lea of node 4 and node 3 For the query {3, 1，4}:
• node 2, 5, 6 are important nodes

2016CCPC东北地区大学生程序设计竞赛 - 重现赛