The Game

Alice and Bob like playing Chinese Chess. One day they are playing a game: Alice has a General, Bob has a General and a Horse, they both obey the rules of Chinese Chess, which are:

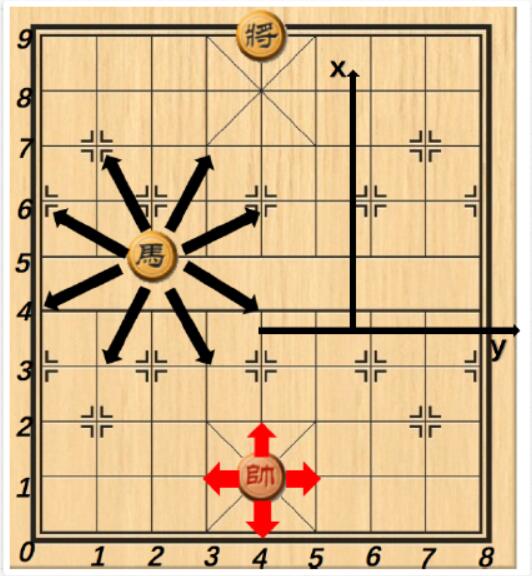
$\bullet $ General has 4 moving directions, Horse has 8 moving directions, but they can't move out of the chess board or their own moving areas. See the picture to get more details:



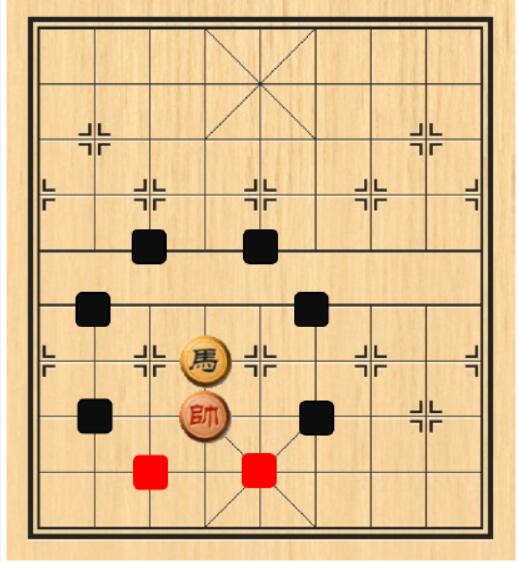
$\bullet $ In some circumstances, Horse can't move to all his positions, just as you can see in the picture, it can move to the black positions, but can't move to the red positions:



$\bullet $ Two Generals can eat each other if and only if they have the same y-coordinate and Horse is not between them.
(For more information, click http://https://en.wikipedia.org/wiki/Xiangqi)

One is considered to be the winner only when his enemy's General is eaten. Please note that if the game is a tie, Alice is considered to be the winner. If Alice know that she has no chance to win the game at the beginning, she will take the strategy to make the game last more steps. If Alice can't win, Bob want to end the game as soon as possible.

If Alice win the game, output "Lucky guy!", else output "Lose in x steps T.T!", x indicates the number of steps they take (the sum of Alice's and Bob's steps). Suppose they all make best strategies.

7 numbers $x_1,y_1,x_2,y_2,x_3,y_3,p$, where:

$\bullet $ $(x_1,y_1)$indicates the coordinate of the Bob's Horse $(0 \leq x_1 \leq 9, 0 \leq y_1 \leq 8)$;
$\bullet $ $(x_2,y_2)$indicates the coordinate of the Bob's General $(7 \leq x_2 \leq 9, 3 \leq y_2 \leq 5)$;
$\bullet $ $(x_3,y_3)$indicates the coordinate of the Alice's General $(0 \leq x_3 \leq 3, 3 \leq y_3 \leq 5)$;

$\bullet $ $p$ indicates the people who moves first, 0 for Alice, 1 for Bob.

If Alice win, output "Lucky guy!" (without quotations), else output “Lose in x steps T.T!”, x indicates the number of steps they take (the sum of Alice's and Bob's steps).

5
0 0 9 3 0 3 0
2 6 9 5 2 3 1
0 4 7 3 1 4 0
3 2 7 4 1 3 0
3 2 7 4 1 3 1 

Lucky guy!
Lose in 3 steps T.T!
Lucky guy!
Lose in 4 steps T.T!
Lose in 1 steps T.T!

In sample 1, Alice moves first, she can eat Bob's General directly;
In sample 2, Bob move his Horse to $(0,5)$, then wherever Alice move her General, it will be eaten by Bob's Horse, so they take 3 steps in total.

2016 ACM/ICPC Asia Regional Shenyang Online