Solid Dominoes Tilings

Dominoes are rectangular tiles with nice 2 × 1 and 1 × 2 sizes.

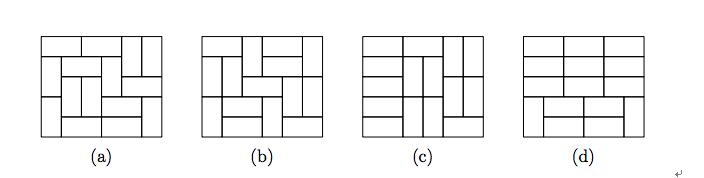
The tiling is called solid if it is not possible to split the tiled rectangle by a straight line, not crossing the interior of any tile. For example, on the picture below the tilings (a) and (b) are solid, while the tilings (c) and (d) are not.



Now the managers of the company wonder, how many different solid tilings exist for an m × n rectangle. Help them to find that out.

The input file contains $m$ and $n (1 \leq m, n \leq 16)$.

Output one integer number mod 1e9+7 - the number of solid tilings of m×n rectangle with 2 × 1 and 1 × 2 pavement tiles.

2 2
5 6
8 7

0
6
13514

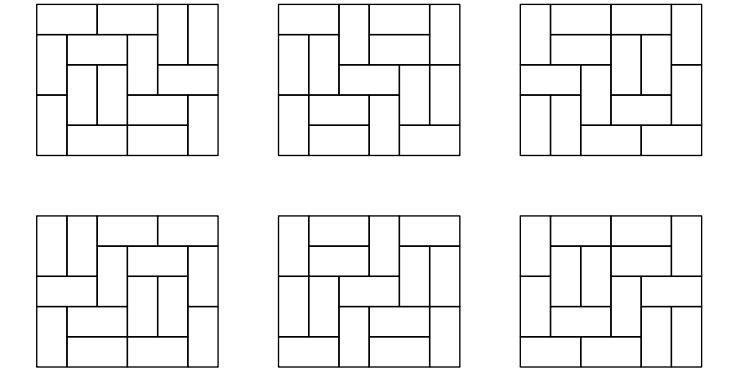
All solid tilings for the 5×6 rectangle are provided on the picture below:

HIT

2016 Multi-University Training Contest 1