Walk Around The Campsite

Gan Jiang was one of Yu Zhou's friends but worked for Cao Cao. One day Gan Jiang visited Yu Zhou's army and would like to steal something from Yu Zhou's army in the midnight. Yu Zhou invited him to stay for the whole night and set up guards.

Gan Jiang saw there are $N$ forts numbered 0, 1, 2, …, n-1 in Yu Zhou's army, the guards are connecting the neighbours forts, including $(0,1), (1,2)...(n-2,n-1), (n-1,0)$ to form a simple polygon. Gan Jiang was in the fort 0 only allowed to walk towards the higher numbered forts in straight line. He was not allowed to go inside of the polygon even pass by other vertices, but he can go along the edges of the polygon, e.g, go from fort 2 to fort 3. When Gan Jiang arrived a fort, he could steal letters of value $V_{i}$. But walking makes him unhappy and for each unit length walking, he will get 1 unit of unhappiness, Gan Jiang could end this mission at any time and ride a horse back to Cao Cao.


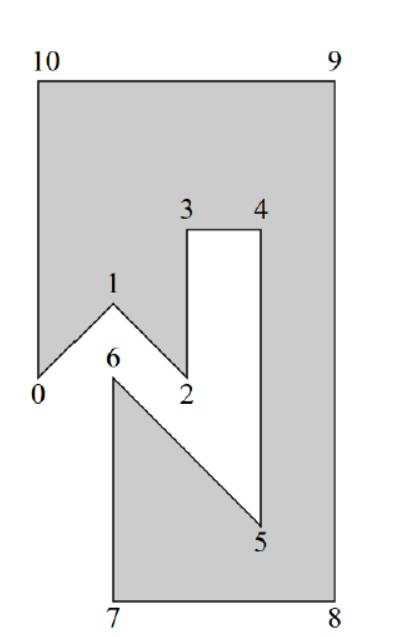
$$Figure\ 1:\ 3_{rd}\ sample$$

Gan Jiang would like to make the total value of letters as big as possible, but make the unhappiness as low as possible. So his target is to make the total value of letters minus total unhappiness as big as possible. Help Gan Jiang to get it.

The first line of the input gives the number of test cases, $T(1≤10)$. $T$ test cases follow. Each test case starts with an integer $N(1≤N≤1000$. Each of the next $N$ lines consists of 3 float numbers with 4 digits after decimal point, $x_{i}$, $y_{i}(-10^{5}≤x_{i},y_{i}≤10^{5})$, $V_{i}(0≤V_{i}≤10^{5})$, $(x_{i},y_{i})$ represents the coordinate of fort $i$ and $V_{i}$ represents the value of the letters in for $i$.

For each test case, output one line containing Case #x: y, where $x$ is the test case number (starting from 1) and $y$ is the maximal value of total value of letters minus total unhappiness. $y$ will be considered correct if it is within an absolute or relative error of $10^{-4}$ of the correct answer.

3

4
0.0000 0.0000 0.0000
1.0000 0.0000 0.5000
1.0000 1.0000 2.0000
0.0000 1.0000 0.5000

5
0.0000 0.0000 0.0000
1.0000 1.0000 0.5000
2.0000 0.0000 2.0000
2.0000 2.0000 3.0000
0.0000 2.0000 0.0000

11
0.0000 0.0000 100.0000
1.0000 1.0000 100.0000
2.0000 0.0000 100.0000
2.0000 2.0000 100.0000
3.0000 2.0000 100.0000
3.0000 -2.0000 100.0000
1.0000 0.0000 100.0000
1.0000 -3.0000 100.0000
4.0000 -3.0000 100.0000
4.0000 4.0000 100.0000
0.0000 4.0000 100.0000

Case #1: 0.5000
Case #2: 1.0000
Case #3: 1070.3431

The 2015 China Collegiate Programming Contest