Count a * b

Marry likes to count the number of ways to choose two non-negative integers $a$ and $b$ less than $m$ to make $a \times b$ mod $m \neq 0$.

Let's denote $f(m)$ as the number of ways to choose two non-negative integers $a$ and $b$ less than $m$ to make $a\times b$ mod $m \neq 0$.

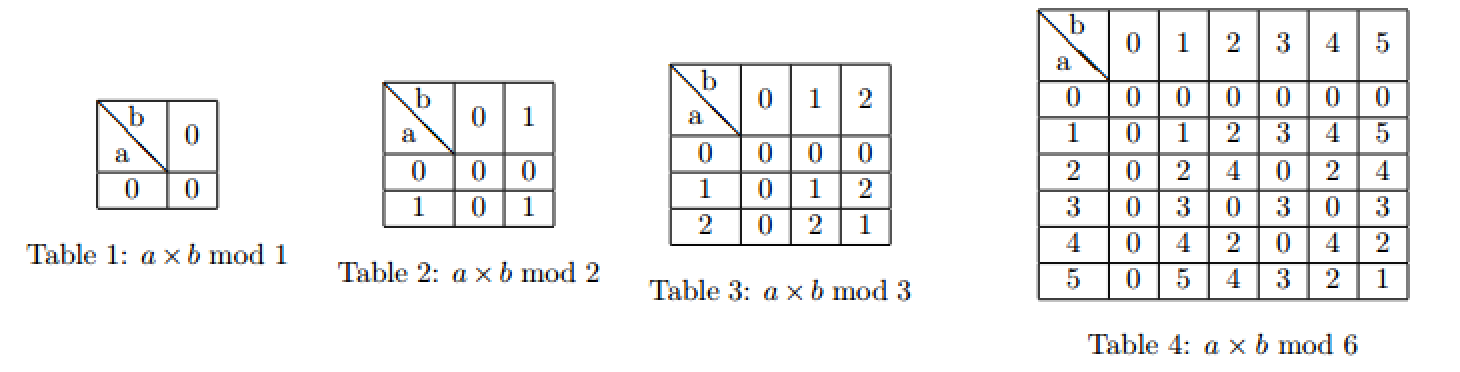
She has calculated a lot of $f(m)$ for different $m$, and now she is interested in another function $g(n)=\sum\limits_{m|n}f(m)$. For example, $g(6)=f(1)+f(2)+f(3)+f(6)=0+1+4+21=26$. She needs you to double check the answer.



Give you $n$. Your task is to find $g(n)$ modulo $2^{64}$.

The first line contains an integer $T$ indicating the total number of test cases. Each test case is a line with a positive integer $n$.

$1 \le T \le 20000$
$1 \le n \le 10^9$

For each test case, print one integer $s$, representing $g(n)$ modulo $2^{64}$.

2
6
514

26
328194

2015ACM/ICPC亚洲区长春站-重现赛（感谢东北师大）