Game of Flying Circus

The discovery of anti-gravitations technology changed the world. The invention of anti-gravitation shoes (Grav-shoes) enables people to fly in the sky freely. This led to the rise of a new sky sport: ``Flying Circus".

Utilizing Grav-shoes and personal flying suits, competitors battle it out in a special field, where they compete scoring obtain $m$ points within a certain time limit. The field is a square with edge length $300$ meters. Moreover, there are four buoys floating at each corner of the square. Four buoys are numbered as $1,2,3,4$ in clockwise order.



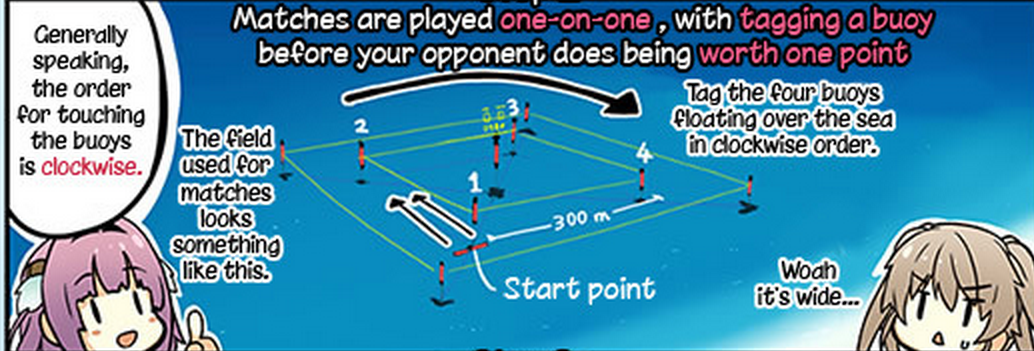
Two players start at buoy $\#1$. When game begin, they will try to touch four floating buoys in clockwise order.
(Since buoy $\#1$ is the start point, the first buoy they need to touch will be buoy $\#2$, and after that, they need to touch buoy $\#3,\#4,\#1$ in order) Note that they could fly freely in the field, even fly inside the square field.

Under two situations the player could score one point.

$\cdot$1. If you touch a buoy before your opponent, you will get one point. For example if your opponent touch the buoy $\#2$ before you after start, he will score one point. So when you touch the buoy $\#2$, you won't get any point. Meanwhile, you cannot touch buoy $\#3$ or any other buoys before touching the buoy $\#2$.

$\cdot$2. Ignoring the buoys and relying on dogfighting to get point. If you and your opponent meet in the same position, you can try to fight with your opponent to score one point. For the proposal of game balance, two players are not allowed to fight before buoy $\#2$ is touched by anybody.

There are three types of players.

Speeder: As a player specializing in high speed movement, he/she tries to avoid dogfighting while attempting to gain points by touching buoys.
Fighter: As a player specializing in dogfighting, he/she always tries to fight with the opponent to score points. Since a fighter is slower than a speeder, it's difficult for him/her to score points by touching buoys when the opponent is a speeder.
All-Rounder: A balanced player between Fighter and Speeder.

There will be a training match between Asuka (All-Rounder) and Shion (Speeder).
Since the match is only a training match, the rules are simplified: the game will end after the buoy $\#1$ is touched by anybody. Shion is a speed lover, and his strategy is very simple: touch buoy $\#2, \#3, \#4, \#1$ along the shortest path.

Asuka is good at dogfighting, so she will always score one point by dogfighting with Shion, and the opponent will be stunned for T seconds after dogfighting. Since Asuka is slower than Shion, she decides to fight with Shion for only one time during the match. It is also assumed that if Asuka and Shion touch the buoy in the same time, the point will be given to Asuka and Asuka could also fight with Shion at the buoy. We assume that in such scenario, the dogfighting must happen after the buoy is touched by Asuka or Shion.

The speed of Asuka is $V_1~m/s$. The speed of Shion is $V_2~m/s$. Is there any possibility for Asuka to win the match (to have higher score)?

The first line contains an integer $t~(0<t\le 1000)$, followed by $t$ lines.
Each line contains three double $T,~V_1$ and $V_2~(0\le V1\le V2\le 2000, 0\le T\le 2000)$ with no more than two decimal places, stands for one case.

If there exist any strategy for Asuka to win the match, output ``Yes", otherwise, output ``No".

2
1 10 13
100 10 13

Case #1: No
Case #2: Yes

Asuka could fly to the mid point of the edge between buoy #2 and buoy #3, and wait there until Shion come. Asuka will fight with Shion when they meet. As a result, Shion will be stunned (It means Shion cannot move for 100 seconds.) Then Asuka could fly back to buoy #2, since the buoy #2 is touched, she will get no point by touching buoy #2. But after that, she could fly to buoy #3, #4, #1 along the edge and get three points.

2015ACM/ICPC亚洲区沈阳站-重现赛（感谢东北大学）