Shape

As we know, a new pentagon shape was found recently that can tile in a plane.

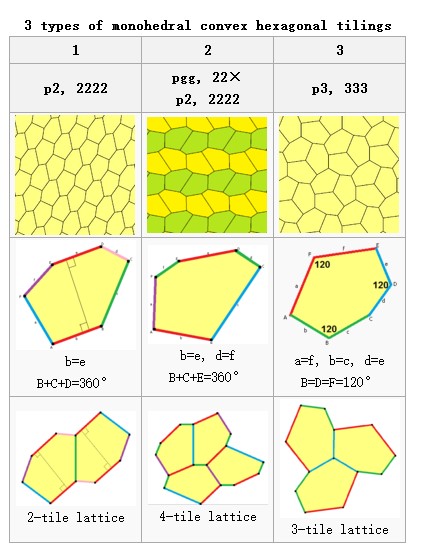
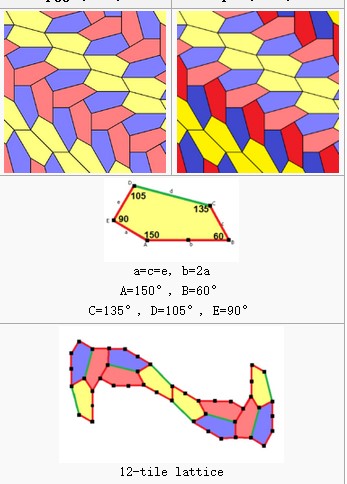
As we can see in the picture, several pentagons form a small unit, which is the minimal repeat unit. And only with translation, we can use these units to cover the whole plane without any gap. However, it is hard to find a new pentagon and its corresponding repeat unit. That’s why the $15^{th}$ pentagon shape was found with the help of computer. We can see how complex it is that it almost cannot be worked out manually.
In this problem, you are going to do a much easier task. You have to write a program to judge whether a given polygon can cover a plane just by translation. You don’t have to handle rotation, symmetry and any other operations, just translation. And you only need to give out your judgment.

The first line of input contains a number $T$ indicating the number of test cases ($T≤50$).
For each test, the first line contains an integer $N$, which indicates the number of the nodes ($3≤N≤20$). And the following $N$ lines give the coordinates $Xi$ and $Yi$ of each node $i$. All the coordinates are integer and the absolute value of each coordinate will not exceed 20. It is guaranteed that the input is a legal polygon, and three consecutive points would not be collinear.

For each test case, output a single line consisting of “Case #X: ” first. $X$ is the test case number starting from 1. Output “Yes” if the given polygon can tile in a plane, or “No” otherwise.

2
4
0 0
0 1
1 1
1 0
5
0 0
1 1
1 2
0 2
-1 1

Case #1: Yes
Case #2: No

2015 ACM/ICPC Asia Regional Hefei Online