
| Online Judge | Online Exercise | Online Teaching | Online Contests | Exercise Author |
|
F.A.Q Hand In Hand Online Acmers |
Best Coder beta VIP | STD Contests DIY | Web-DIY beta |
Solve this interesting problem
Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)Total Submission(s): 3633 Accepted Submission(s): 1187
Problem Description
Have you learned something about segment tree? If not, doní»t worry, I will explain it for you.
Segment Tree is a kind of binary tree, it can be defined as this:
- For each node u in Segment Tree, u has two values: $L_u$ and $R_u$.
- If $L_u = R_u$, u is a leaf node.
- If $L_u \neq R_u$, u has two children x and y,with $L_x = L_u$,$R_x = \lfloor \frac{L_u + R_u }{2}\rfloor$,$L_y = \lfloor \frac{L_u + R_u }{2}\rfloor + 1$,$R_y = R_u$.
Here is an example of segment tree to do range query of sum.
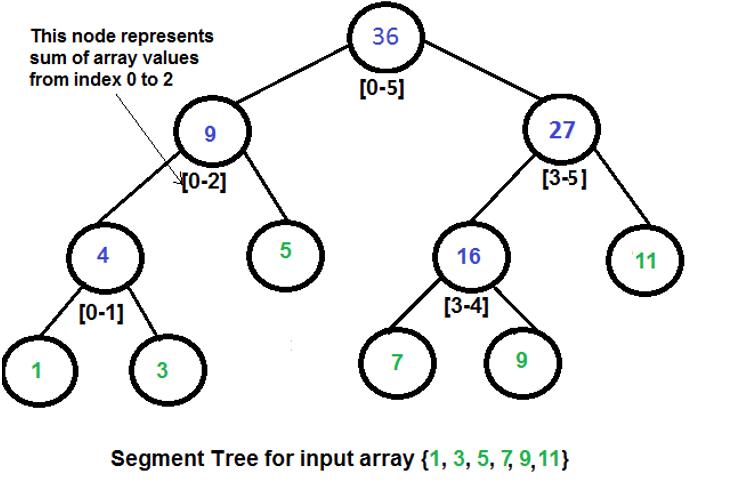
Given two integers L and R, Your task is to find the minimum non-negative n satisfy that: A Segment Tree with root node's value $L_{root} = 0$ and $R_{root} = n$ contains a node u with $L_u = L$ and $R_u = R$.
Segment Tree is a kind of binary tree, it can be defined as this:
- For each node u in Segment Tree, u has two values: $L_u$ and $R_u$.
- If $L_u = R_u$, u is a leaf node.
- If $L_u \neq R_u$, u has two children x and y,with $L_x = L_u$,$R_x = \lfloor \frac{L_u + R_u }{2}\rfloor$,$L_y = \lfloor \frac{L_u + R_u }{2}\rfloor + 1$,$R_y = R_u$.
Here is an example of segment tree to do range query of sum.

Given two integers L and R, Your task is to find the minimum non-negative n satisfy that: A Segment Tree with root node's value $L_{root} = 0$ and $R_{root} = n$ contains a node u with $L_u = L$ and $R_u = R$.
Input
The input consists of several test cases.
Each test case contains two integers L and R, as described above.
$0 \leq L \leq R \leq 10^9$
$\frac{L}{R-L+1} \leq 2015$
Each test case contains two integers L and R, as described above.
$0 \leq L \leq R \leq 10^9$
$\frac{L}{R-L+1} \leq 2015$
Output
For each test, output one line contains one integer. If there is no such n, just output -1.
Sample Input
6 7 10 13 10 11
Sample Output
7 -1 12
Author
ZSTU
Source
| Home | Top |
Hangzhou Dianzi University Online Judge 3.0 Copyright © 2005-2024 HDU ACM Team. All Rights Reserved. Designer & Developer : Wang Rongtao LinLe GaoJie GanLu Total 0.000000(s) query 1, Server time : 2024-11-22 08:17:54, Gzip enabled |
Administration |