
| Online Judge | Online Exercise | Online Teaching | Online Contests | Exercise Author |
|
F.A.Q Hand In Hand Online Acmers |
Best Coder beta VIP | STD Contests DIY | Web-DIY beta |
Trie
Time Limit: 12000/6000 MS (Java/Others) Memory Limit: 262144/262144 K (Java/Others)Total Submission(s): 774 Accepted Submission(s): 110
Problem Description
Little Bob studied Trie in Data Structure class. He learned that Trie is a rooted tree to store some strings. There is a character on each edge of a Trie. (In this problem, the valid characters are lowercase Latin letters.)
Bob draws a Trie with n nodes, and the nodes are numbered with integers from 1 to n. The number of the root node is always 1.
He uses Si to denote the string concatenated with characters on the path from the root to node i. It can be seen that S1 is the empty string. Furthermore, for a set P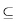 {1, 2, . . . , n}, SP = {Si | i
{1, 2, . . . , n}, SP = {Si | i 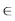 P}.
P}.
Bob defines a kind of trait on this Trie. The trait can be described with a set P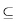 {1, 2, . . . , n}. We say a string a has this trait, if and only if there exists a string b
{1, 2, . . . , n}. We say a string a has this trait, if and only if there exists a string b 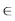 SP such that a ends with b. Here string a ends with string b means the last |b| characters of a is exactly b. (Note that every string ends with the empty string).
SP such that a ends with b. Here string a ends with string b means the last |b| characters of a is exactly b. (Note that every string ends with the empty string).
Bob also defines a mapping f on P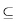 {1, 2, ..., n}, and f (P) is also a subset of {1, 2, . . . , n}. i
{1, 2, ..., n}, and f (P) is also a subset of {1, 2, . . . , n}. i 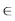 f (P) if and only if there exists j
f (P) if and only if there exists j 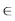 P such that Sj ends with Si.
P such that Sj ends with Si.
Initially, there is no traits been defined. Bob will add traits whenever he wants. Let Di denote the number of traits that Si has until now. Note that Di may change when a new trait is added.
Besides adding new traits, Bob may also ask you something about his Trie. In each query, Bob will give you a set P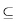 {1, 2, . . . , n}, and you need to compute
{1, 2, . . . , n}, and you need to compute 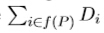 . Are you willing to do this for Bob?
. Are you willing to do this for Bob?
Bob draws a Trie with n nodes, and the nodes are numbered with integers from 1 to n. The number of the root node is always 1.
He uses Si to denote the string concatenated with characters on the path from the root to node i. It can be seen that S1 is the empty string. Furthermore, for a set P
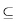 {1, 2, . . . , n}, SP = {Si | i
{1, 2, . . . , n}, SP = {Si | i 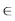 P}.
P}.Bob defines a kind of trait on this Trie. The trait can be described with a set P
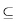 {1, 2, . . . , n}. We say a string a has this trait, if and only if there exists a string b
{1, 2, . . . , n}. We say a string a has this trait, if and only if there exists a string b 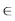 SP such that a ends with b. Here string a ends with string b means the last |b| characters of a is exactly b. (Note that every string ends with the empty string).
SP such that a ends with b. Here string a ends with string b means the last |b| characters of a is exactly b. (Note that every string ends with the empty string).Bob also defines a mapping f on P
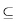 {1, 2, ..., n}, and f (P) is also a subset of {1, 2, . . . , n}. i
{1, 2, ..., n}, and f (P) is also a subset of {1, 2, . . . , n}. i 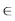 f (P) if and only if there exists j
f (P) if and only if there exists j 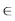 P such that Sj ends with Si.
P such that Sj ends with Si.Initially, there is no traits been defined. Bob will add traits whenever he wants. Let Di denote the number of traits that Si has until now. Note that Di may change when a new trait is added.
Besides adding new traits, Bob may also ask you something about his Trie. In each query, Bob will give you a set P
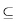 {1, 2, . . . , n}, and you need to compute
{1, 2, . . . , n}, and you need to compute 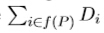 . Are you willing to do this for Bob?
. Are you willing to do this for Bob?Input
The first line contains an integer T (T ≤ 5), denoting the number of the test cases.
For each test case, the first line contains an integer n(1 ≤ n ≤ 105).
From the second to the n-th line, this n - 1 lines describe Bob' s Trie. The i-th line contains an integer u(u < i), and a lowercase letter c, which means that the father of node i is node u and the character on that edge is c. We ensure that for each node i, letters on edges connecting i and its children are all different.
The next line contains an integer m(m ≤ 105), which means there are m operations.
The next m lines describe all operations. In each line, the first integer indicates the type of this operation. 1 means Bob will add a new trait and 2 means Bob is asking you a question. The second integer k is the size of set P , and the next k integers are the elements of P. We ensure that these k integers are different, and they are all between 1 and n. The total size of the m sets will not be larger than 5·105.
For each test case, the first line contains an integer n(1 ≤ n ≤ 105).
From the second to the n-th line, this n - 1 lines describe Bob' s Trie. The i-th line contains an integer u(u < i), and a lowercase letter c, which means that the father of node i is node u and the character on that edge is c. We ensure that for each node i, letters on edges connecting i and its children are all different.
The next line contains an integer m(m ≤ 105), which means there are m operations.
The next m lines describe all operations. In each line, the first integer indicates the type of this operation. 1 means Bob will add a new trait and 2 means Bob is asking you a question. The second integer k is the size of set P , and the next k integers are the elements of P. We ensure that these k integers are different, and they are all between 1 and n. The total size of the m sets will not be larger than 5·105.
Output
For each test case, output the answer for each query operation, one answer in a line.
Sample Input
1 6 1 a 1 b 1 c 3 a 3 b 5 1 2 3 4 2 2 5 6 1 2 2 3 2 2 4 5 2 1 6
Sample Output
2 3 4
Source
| Home | Top |
Hangzhou Dianzi University Online Judge 3.0 Copyright © 2005-2025 HDU ACM Team. All Rights Reserved. Designer & Developer : Wang Rongtao LinLe GaoJie GanLu Total 0.000000(s) query 1, Server time : 2025-04-01 09:08:03, Gzip enabled |
Administration |