
| Online Judge | Online Exercise | Online Teaching | Online Contests | Exercise Author |
|
F.A.Q Hand In Hand Online Acmers |
Best Coder beta VIP | STD Contests DIY | Web-DIY beta |
Square
Time Limit: 24000/12000 MS (Java/Others) Memory Limit: 262144/262144 K (Java/Others)Total Submission(s): 447 Accepted Submission(s): 302
Problem Description
Nothing is more beautiful than square! So, given a grid of cells, each cell being black or white, it is reasonable to evaluate this grid¡¯s beautifulness by the side length of its maximum continuous subsquare which fully consists of white cells.
Now you¡¯re given an N ¡Á N grid, and the cells are all black. You can paint some cells white. But other cells are broken in the sense that they cannot be paint white. For each integer i between 0 and N inclusive, you want to find the number of different painting schemes such that the beautifulness is exactly i. Two painting schemes are considered different if and only if some cells have different colors. Painting nothing is considered to be a scheme.
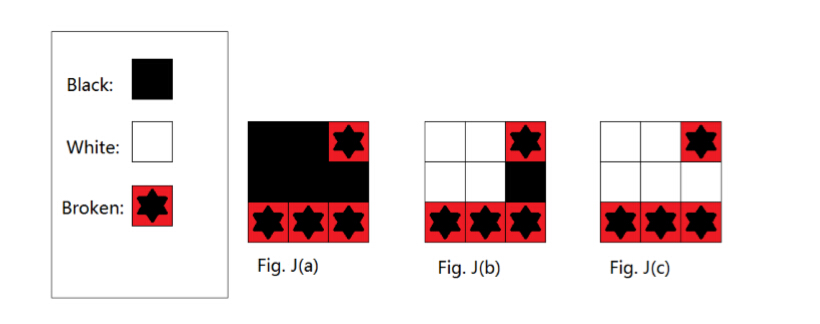
For example, N = 3 and there are 4 broken cells as shouwn in Fig. J(a). There are 2 painting schemes for i=2 as shown in Fig. J(b) and J(c).
You just need to output the answer modulo 109 + 7.
Now you¡¯re given an N ¡Á N grid, and the cells are all black. You can paint some cells white. But other cells are broken in the sense that they cannot be paint white. For each integer i between 0 and N inclusive, you want to find the number of different painting schemes such that the beautifulness is exactly i. Two painting schemes are considered different if and only if some cells have different colors. Painting nothing is considered to be a scheme.

For example, N = 3 and there are 4 broken cells as shouwn in Fig. J(a). There are 2 painting schemes for i=2 as shown in Fig. J(b) and J(c).
You just need to output the answer modulo 109 + 7.
Input
The first line contains an integer T (T ¡Ü 10) denoting the number of the test cases.
For each test case, the first line contains an integer N (1 ¡Ü N ¡Ü 8), denoting the size of the grid is N ¡Á N . Then N lines follow, each line containing an N-character string of ¡°o¡± and ¡°*¡±, where ¡°o¡± stands for a paintable cell and ¡°*¡± for a broken cell.
For each test case, the first line contains an integer N (1 ¡Ü N ¡Ü 8), denoting the size of the grid is N ¡Á N . Then N lines follow, each line containing an N-character string of ¡°o¡± and ¡°*¡±, where ¡°o¡± stands for a paintable cell and ¡°*¡± for a broken cell.
Output
For each test case, for each integer i between 0 and N inclusive, output the answer in a single line.
Sample Input
2 3 oo* ooo *** 8 oooooooo oooooooo oooooooo oooooooo oooooooo oooooooo oooooooo oooooooo
Sample Output
1 29 2 0 1 401415247 525424814 78647876 661184312 550223786 365317939 130046 1
Source
| Home | Top |
Hangzhou Dianzi University Online Judge 3.0 Copyright © 2005-2024 HDU ACM Team. All Rights Reserved. Designer & Developer : Wang Rongtao LinLe GaoJie GanLu Total 0.000000(s) query 1, Server time : 2024-11-22 02:31:08, Gzip enabled |
Administration |