Little Pony and Boast Busters

"I hereby challenge you, Ponyvillians: anything you can do, I can do better. Any takers? Anyone? Or is Trixie destined to be the greatest equine who has ever lived!?!" — "Boast Busters"

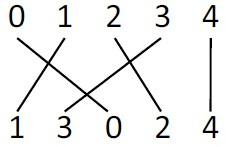
Given two permutation P₀ && P₁ of {0, 1, ..., n - 1}, we define the crossing number of it as follows. Write P₀ from left to right above P₁ and draw a straight line between each same elements. The crossing number of P₀ and P₁ is the number of pairs of lines that cross.

For example, if n = 5, and P₀ = {0, 1, 2, 3, 4}, and P₁ = {1, 3, 0, 2, 4}, then the crossing number of P₀ and P₁ is 3, as shown in the figure below.


Now given you the two permutation, you need to implement the following operations:

SWAP p a b: swap P_p[a] and P_p[b] (0<=p<=1, 0<=a, b<=n-1).

QUERY: ask the crossing number of the current P₀ and P₁.

Input contains multiple test cases (less than 10). For each test case, the first line contains one integer n (1<=n<=10^5).
The second line contains n integers P₀[0], P₀[1], ..., P₀[n-1].
The third line contains n integers P₁[0], P₁[1], ..., P₁[n-1].
The next line contains one integer q —— the number of operations (1<=q<=10^5). The next q line, each line will contains a operation as we mentioned above.

For each query, output the corresponding result in one line.

5
0 1 2 3 4
1 3 0 2 4
5
QUERY
SWAP 1 2 4
QUERY
SWAP 0 2 4
QUERY

3
6
5

BestCoder Round #7