
| Online Judge | Online Exercise | Online Teaching | Online Contests | Exercise Author |
|
F.A.Q Hand In Hand Online Acmers |
Best Coder beta VIP | STD Contests DIY | Web-DIY beta |
Robbery Plan
Time Limit: 7000/3500 MS (Java/Others) Memory Limit: 262144/262144 K (Java/Others)Total Submission(s): 140 Accepted Submission(s): 26
Problem Description
As the chief consultant in the International Consulting Company, you¡¯re now enjoying such a high reputation in the industry that even the organizations underworld often come to you and ask for your suggestions. Professional as you are to your clients, you always try your best to help them and, certainly, make more profits for yourself. Money makes the mare go, and you¡¯re no exception either.
But the shareholders of the company are always watching their profits as well. In order to protect the investors, they keep focusing on every project you take charge of. Once you receive money in a project, they will come immediately to you. If your profit is less than M dollars, they won¡¯t step in; but if the profit reaches M , they will meddle in and take away profits in unit of M as much as possible. (e.g. if you earn (2M + 1) or exactly 2M dollars, they will both take 2M away.)
Now a big client comes. A famous robbery organization expects you to help them construct a robbery plan. The offer is so irresistible that you accept it immediately.
Their targets are the banks in the city. Totally, there¡¯re K banks (numbered from 1 to K) that located at different areas, which produce different difficulties to rob them. The robbery team is made up of N people, and they have totally Q dollars as action funds. In a robbery, if they send p people and spend d dollars of funds to rob bank i, they will earn fi[p, d] in this action. Here, fi[p, d] is generated by
fi[p, d] =0 (p <= 0 or d <= 0)
fi[p, d] = fi[p - 1, d - ei] + fi[p - 1, d] (1 < p <= N,1 <= d <= Q)
and fi[1, d] comes from
fi[1, d] = Aif2i[1, d - 1] + Bifi[1, d - 1] + Ci (1 <= d <= Q)
where ei, Ai, Bi, Ci are coefficients given initially.
The team is so professional (as you are) that the members always succeed in robberies. After they rob a bank and get the money, the team will divide it into (almost) equal parts and distribute them to you and everyone who participates in this action. That is, if they send p men and rob X dollars, you¡¯ll receive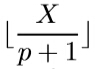 dollars immediately after the robbery on this bank. But at the time you receive the money, the damned shareholders will come and take away the part of theirs. Only the remaining part belongs to you.
dollars immediately after the robbery on this bank. But at the time you receive the money, the damned shareholders will come and take away the part of theirs. Only the remaining part belongs to you.
You¡¯re now required to help them determine the plan. Note that the robberies won¡¯t take place simultaneously; and thus each person can rob several banks, but each bank can be robbed at most once (if we choose to rob it). The money they rob won¡¯t be added to their action funds afterwards. Your final profit equals to the sum of profits that belongs to you after each robbery (Note that your total profit will not be checked again by the shareholders, i.e. your total profit may exceed M ).
Your target, professionally speaking, is to maximize the total profit of yourself after they finish robbing the banks according to your plan. Be careful of the annoying shareholders in the company!
But the shareholders of the company are always watching their profits as well. In order to protect the investors, they keep focusing on every project you take charge of. Once you receive money in a project, they will come immediately to you. If your profit is less than M dollars, they won¡¯t step in; but if the profit reaches M , they will meddle in and take away profits in unit of M as much as possible. (e.g. if you earn (2M + 1) or exactly 2M dollars, they will both take 2M away.)
Now a big client comes. A famous robbery organization expects you to help them construct a robbery plan. The offer is so irresistible that you accept it immediately.
Their targets are the banks in the city. Totally, there¡¯re K banks (numbered from 1 to K) that located at different areas, which produce different difficulties to rob them. The robbery team is made up of N people, and they have totally Q dollars as action funds. In a robbery, if they send p people and spend d dollars of funds to rob bank i, they will earn fi[p, d] in this action. Here, fi[p, d] is generated by
fi[p, d] =0 (p <= 0 or d <= 0)
fi[p, d] = fi[p - 1, d - ei] + fi[p - 1, d] (1 < p <= N,1 <= d <= Q)
and fi[1, d] comes from
fi[1, d] = Aif2i[1, d - 1] + Bifi[1, d - 1] + Ci (1 <= d <= Q)
where ei, Ai, Bi, Ci are coefficients given initially.
The team is so professional (as you are) that the members always succeed in robberies. After they rob a bank and get the money, the team will divide it into (almost) equal parts and distribute them to you and everyone who participates in this action. That is, if they send p men and rob X dollars, you¡¯ll receive
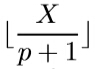 dollars immediately after the robbery on this bank. But at the time you receive the money, the damned shareholders will come and take away the part of theirs. Only the remaining part belongs to you.
dollars immediately after the robbery on this bank. But at the time you receive the money, the damned shareholders will come and take away the part of theirs. Only the remaining part belongs to you.You¡¯re now required to help them determine the plan. Note that the robberies won¡¯t take place simultaneously; and thus each person can rob several banks, but each bank can be robbed at most once (if we choose to rob it). The money they rob won¡¯t be added to their action funds afterwards. Your final profit equals to the sum of profits that belongs to you after each robbery (Note that your total profit will not be checked again by the shareholders, i.e. your total profit may exceed M ).
Your target, professionally speaking, is to maximize the total profit of yourself after they finish robbing the banks according to your plan. Be careful of the annoying shareholders in the company!
Input
The input consists of several test cases. The first line of input gives the number of test cases T (T<=5).
For each test case:
The first line consists of four integers N, Q, K(1<=N<=1000, 1<=Q<=20, 1<=K<=50) and M (1<=M<=106).
The following K lines describe the property of banks, where the ith line contains ei, Ai, Bi, Ci(1<=ei<=Q, 1<=Ai, Bi, Ci<=109) in order.
For each test case:
The first line consists of four integers N, Q, K(1<=N<=1000, 1<=Q<=20, 1<=K<=50) and M (1<=M<=106).
The following K lines describe the property of banks, where the ith line contains ei, Ai, Bi, Ci(1<=ei<=Q, 1<=Ai, Bi, Ci<=109) in order.
Output
For each test case, output the maximum profits you can obtain in a line.
Sample Input
1 80 10 1 1000000 1 988123 894129 102939
Sample Output
999996
Author
BUPT
Source
| Home | Top |
Hangzhou Dianzi University Online Judge 3.0 Copyright © 2005-2024 HDU ACM Team. All Rights Reserved. Designer & Developer : Wang Rongtao LinLe GaoJie GanLu Total 0.000000(s) query 1, Server time : 2024-11-22 12:58:18, Gzip enabled |
Administration |