One to Four

Given one n * m matrix consist of only positive numbers, It is guaranteed that the product of n and m is a multiple of 4, therefore, we can divide it into four identical parts(that is, every part is a 4-connected subset and we can obtain each part from each other by rotation and translation, every element must be included in exactly one part).


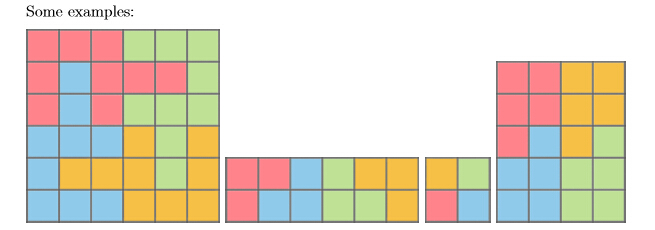
(Grids that from the same part are labeled by the same colour, all four partitions above are valid.)
Note that the partition below is NOT valid because we can only use translation and rotation, no symmetrical reverse:

Once we choose a partition, we can choose some translation and rotation to make these four parts coincide, finally we add up every four values lying on the same grid and choose the minimum sum as the score of the partition and transformation.
Now you're given the matrix, your task is to choose a proper partition and transformation to get the maximum score.

There are several testcases, please process till EOF.
In each test case, first line contains two integers n and m. Following n lines each contains m integers A_ij, describing the matrix.
1 ≤ n,m ≤ 30,1 ≤ A_ij ≤ 10000.

For each testcase output one line contains one integer: the maximum score you can get.

2 4
1 1 1 1
2 2 2 2
4 4
1 1 1 3
2 1 3 3
2 2 4 3
2 4 4 4

6
10

Fudan University

2014 Multi-University Training Contest 3