
| Online Judge | Online Exercise | Online Teaching | Online Contests | Exercise Author |
|
F.A.Q Hand In Hand Online Acmers |
Best Coder beta VIP | STD Contests DIY | Web-DIY beta |
Clumsy Algorithm
Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)Total Submission(s): 283 Accepted Submission(s): 95
Problem Description
¡¡¡¡Sorted Lists are thought beautiful while permutations are considered elegant. So what about sequence (1, 2, ... , n) ? It is the oracle from god. Now Coach Pang finds a permutation (p1, p2, ... , pn) over {1, 2, ... , n} which has been shuffled by some evil guys. To show Coach Pang¡¯s best regards to the oracle, Coach Pang decides to rearrange the sequence such that it is the same as (1, 2, 3, ... , n). The time cost of swapping pi and pj is 2|i- j| - 1. Of course, the minimum time cost will be paid since Coach Pang is lazy and busy. Denote the minimum time cost of the task as f(p). But Coach Pang is not good at maths. He finally works out a clumsy algorithm to get f(p) as following:
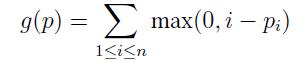
¡¡¡¡Coach Pang¡¯s algorithm is clearly wrong. For example, n = 3 and (3, 2, 1) is the permutation. In this case, f(p) = 3 but g(p) = 0 + 0 + 2 = 2. The question is that how many permutations p of {1, 2, ... , n} such that f(p) = g(p). To make the problem more challenge, we also restrict the prefix of p to (a1, a2, ... , ak). To sum up, you need to answer the question that how many permutations p of {1, 2, ... , n} with the fixed prefix p1 = a1, p2 = a2, ... , pk = ak such that f(p) = g(p). Since the answer may be very large, for convenience, you are only asked to output the remainder divided by (109 + 7).
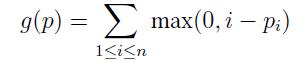
¡¡¡¡Coach Pang¡¯s algorithm is clearly wrong. For example, n = 3 and (3, 2, 1) is the permutation. In this case, f(p) = 3 but g(p) = 0 + 0 + 2 = 2. The question is that how many permutations p of {1, 2, ... , n} such that f(p) = g(p). To make the problem more challenge, we also restrict the prefix of p to (a1, a2, ... , ak). To sum up, you need to answer the question that how many permutations p of {1, 2, ... , n} with the fixed prefix p1 = a1, p2 = a2, ... , pk = ak such that f(p) = g(p). Since the answer may be very large, for convenience, you are only asked to output the remainder divided by (109 + 7).
Input
¡¡¡¡The first line contains a positive integer T(1 <= T <= 100), which indicates the number of test cases. T lines follow. Each line contains n, k, a1, a2, a3, ... , ak. (1 <= n <= 100, 0 <= k <= n, 1 <= ai <= n and all ai are distinct.)
Output
¡¡¡¡For each test case, output one line ¡°Case #x: y¡±, where x is the case number (starting from 1) and y is the answer to each test case.
Sample Input
2 3 0 5 2 1 4
Sample Output
Case #1: 5 Case #2: 3
Hint
Among all permutations over {1, 2, 3}, {3, 2, 1} is the only counter-example.
Source
| Home | Top |
Hangzhou Dianzi University Online Judge 3.0 Copyright © 2005-2024 HDU ACM Team. All Rights Reserved. Designer & Developer : Wang Rongtao LinLe GaoJie GanLu Total 0.000000(s) query 1, Server time : 2024-11-23 08:04:42, Gzip enabled |
Administration |