Candy Factory

  A new candy factory opens in pku-town. The factory import M machines to produce high quality candies. These machines are numbered from 1 to M.
  There are N candies need to be produced. These candies are also numbered from 1 to N. For each candy i , it can be produced in any machine j. It also has a producing time(s_i,t_i) , meaning that candy i must start producing at time s_i and will finish at t_i. Otherwise if the start time is p_i(s_i < p_i < t_i) then candy will still finish at t_i but need additional K*(p_i - s_i) cost. The candy can’t be produced if p_i is greater than or equal to t_i. Of course one machine can only produce at most one candy at a time and can’t stop once start producing.
  On the other hand, at time 0 all the machines are in their initial state and need to be “set up” or changed before starting producing. To set up Machine j from its initial state to the state which is suitable for producing candiy i, the time required is C_ij and cost is D_ij. To change a machine from the state suitable for candy i₁ into the state suitable for candy i₂, time required is E_i1i2 and cost is F_i1i2.
  As the manager of the factory you have to make a plan to produce all the N candies. While the sum of producing cost should be minimized.

　　There are multiple test cases.
　　For each case, the first line contains three integers N(1<=N<=100), M(1<=M<=100), K(1<=K<=100) . The meaning is described above.
　　Then N lines follow, each line contains 2 integers s_i and t_i(0 <= s_i < t_i <100000).
　　Then N lines follow, each line contains M integers, the j-th integer of the i-th line indicating C_ij(1<=C_ij<=100000) .
　　Then N lines follow, each line contains M integers, the j-th integer of the i-th line indicating D_ij(1<=D_ij<=100000) .
　　Then N lines follow, each line contains N integers, the i₂-th integer of the i₁-th line indicating E_i1i2(1<=E_i1j2<=100000) .
　　Then N lines follow, each line contains N integers, the i₂-th integer of the i₁-th line indicating F_i1i2(1 <= F_i1j2<=100000) .
　　Since the same candy will only be produced once, E_ii and F_ii are meaningless and will always be -1.
　　The input ends by N=0 M=0 K=0. Cases are separated with a blank line.

  For each test case, if all of M candies can be produced, output the sum of minimum producing cost in a single line. Otherwise output -1.

3 2 1
4 7
2 4
8 9
4 4
3 3
3 3
2 8
12 3
14 6
-1 1 1
1 -1 1
1 1 -1
-1 5 5
5 -1 5
5 5 -1

1 1 2
1 5
5
5
-1
-1

0 0 0

11
-1

For the first example, the answer can be achieved in the following way:

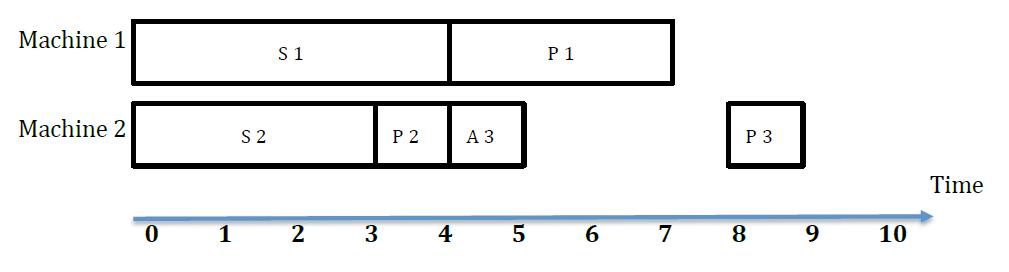
  In the picture, S i represents setting up time for candy i, A i represents changing time for candy i and P i represents producing time for candy i .
  So the total cost includes:
　　setting up machine 1 for candy 1, costs 2
　　setting up machine 2 for candy 2, costs 3
　　changing state from candy 2 to candy 3, costs 5
　　late start of candy 2, costs 1

2013 Asia Hangzhou Regional Contest