
| Online Judge | Online Exercise | Online Teaching | Online Contests | Exercise Author |
|
F.A.Q Hand In Hand Online Acmers |
Best Coder beta VIP | STD Contests DIY | Web-DIY beta |
G(x)
Time Limit: 2000/500 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)Total Submission(s): 829 Accepted Submission(s): 210
Problem Description
For a binary number x with n digits (AnAn-1An-2 ... A2A1), we encode it as 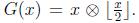
Where "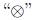 " is bitwise XOR operation and "
" is bitwise XOR operation and "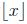 " indicates the largest integer which is not greater than x.
" indicates the largest integer which is not greater than x.
Due to some reasons, Mzry1992 encode his password P into G(P), and additionally, he encode P + 1 into G(P + 1) too, and write G(P) and G(P + 1) into his diary.
This story happened many years ago and now you hold the diary with these numbers in your hands. Unfortunately, some digits are unreadable now. Could you determine the values of these digits using the readable digits?
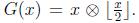
Where "
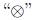 " is bitwise XOR operation and "
" is bitwise XOR operation and "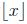 " indicates the largest integer which is not greater than x.
" indicates the largest integer which is not greater than x.Due to some reasons, Mzry1992 encode his password P into G(P), and additionally, he encode P + 1 into G(P + 1) too, and write G(P) and G(P + 1) into his diary.
This story happened many years ago and now you hold the diary with these numbers in your hands. Unfortunately, some digits are unreadable now. Could you determine the values of these digits using the readable digits?
Input
The first line has a number T (T <= 100) , indicating the number of test cases.
For every test case, it has 2 lines of same number of digits describe G(P) and G(P + 1), In every line, it only contains 1, 0 and ?. Unreadable digits are denoted with symbol ?, The length of every line in the input is up to 105.
For every test case, it has 2 lines of same number of digits describe G(P) and G(P + 1), In every line, it only contains 1, 0 and ?. Unreadable digits are denoted with symbol ?, The length of every line in the input is up to 105.
Output
For every case, you should output "Case #t: " at first, without quotes. The t is the case number starting from 1.
Then, if there is impossible to restore G(P) and G(P + 1), you should output "Impossible" in the second line.
Otherwise, if G(P) is unique, you should output restored G(P) and G(P +1) in the same format.
Otherwise, you should output "Ambiguous" and the number of possible G(P) in the second line.
The number may be very large so the answer should modulo 10^9 + 7.
Then, if there is impossible to restore G(P) and G(P + 1), you should output "Impossible" in the second line.
Otherwise, if G(P) is unique, you should output restored G(P) and G(P +1) in the same format.
Otherwise, you should output "Ambiguous" and the number of possible G(P) in the second line.
The number may be very large so the answer should modulo 10^9 + 7.
Sample Input
3 10?? 10?? 0010 0110 1?01 0?01
Sample Output
Case #1: Ambiguous 3 Case #2: 0010 0110 Case #3: Impossible
Hint
In the first sample case, the three possible situations are:
1.
G(12) = 1010
G(13) = 1011
2.
G(13) = 1011
G(14) = 1001
3.
G(14) = 1001
G(15) = 1000
Source
| Home | Top |
Hangzhou Dianzi University Online Judge 3.0 Copyright © 2005-2024 HDU ACM Team. All Rights Reserved. Designer & Developer : Wang Rongtao LinLe GaoJie GanLu Total 0.000000(s) query 1, Server time : 2024-11-22 12:01:38, Gzip enabled |
Administration |