Rectangles

　　There is a big N * M rectangle consists of N * M unit squares, and each unit square has an integer value 0 or 1 on it. N and M may be very large, but the number of unit squares which have value 1 on it, is not more than 100.
　　You task is to calculate how many different rectangles (which consist of some complete unit squares) satisfy that the values on its unit squares are all 0.
　　We say two rectangles are different if and only if they have different size or they are in different location.

　　There is an integer T (1 <= T <= 200) in the first line, which indicates that there are T test cases in total.
　　For each test case, there are three integers N (1 <= N <= 1000000000), M (1 <= M <= 1000000000), K (0 <= K <= 100, K <= N * M). N and M have the same meanings as above. K means there are exactly K unit squares which have value 1 on it, surely that the other unit squares have value 0 on it. Then there are following K lines and each line has two integer x (1 <= x <= N), y (1 <= y <= M), means that the unit square in row x and column y has value 1 on it. You can assume that no two pairs of x and y are the same.
There are at most 10 test cases that satisfy N > 100 or M > 100 or K > 15.

　　For each test case, you should output the correct answer of the above task.
　　Because the answer may be very large, you should just output the remainder of it divided by 1000000007 instead.

3
1 1 0
2 2 0
2 3 2
1 1
2 3

1
9
7

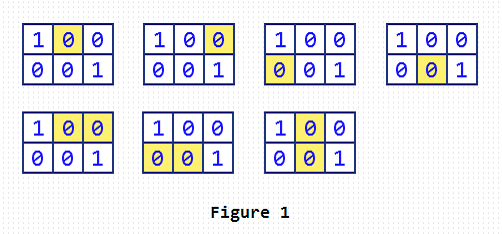
For Sample 3, the yellow unit squares in Figure 1 show you the 7 rectangles.

A Contest to Celebrate Girlfriend's Birthday by Staginner