
| Online Judge | Online Exercise | Online Teaching | Online Contests | Exercise Author |
|
F.A.Q Hand In Hand Online Acmers |
Best Coder beta VIP | STD Contests DIY | Web-DIY beta |
Programming the EDSAC
Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)Total Submission(s): 195 Accepted Submission(s): 73
Problem Description
The world's first full-scale, stored-program, electronic, digital computer was the EDSAC (Electronic Delay Storage Automatic Calculator). The EDSAC had an accumulator-based instruction set, operating on 17-bit words(and 35-bit double words), and used a 5-bit teletypewriter code for input and output.
The EDSAC was programmed using a very simple assembly language: a single letter opcode followed by an unsigned decimal address, followed by the the letter "F"(for full word) or "D"(for double word). For example, the instruction "A 128 F" would mean "add the full word at location 128 to the accumulator", and would be assembled into the 17-bit binary value, 11100000100000000, consisting of a 5-bit opcode(11100="add"), an 11-bit operand (00010000000 = 128), and a single 0 bit denoting a full word operation(a 1 bit would indicate a double word operation).
Although arithmetic on the EDSAC was fixed point two's complement binary, it was not mere intger arithmetic (as is common with modern machines). The EDSAC hardware assumed a binary point between the lrftmost bit and its immediate successor. Thus the hardware could handle only values in the range -1.0 <= x < 1.0 . For example:

As you can see, the largest possible positive value was:
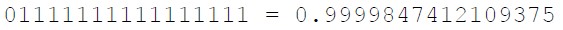
and the smallest possible positive value was:
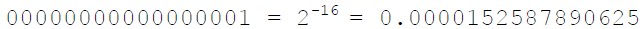
(This also happens to be the increment between successive values on the EDSAC).
By a curious coincidence(or an elegant design decision), the opcode for the add operation(11100) was the same as the teleprinter code for the letter"A". The opcode for subtract was the same as the teleprinter code for "S"(01100), and so on. This simplified the programming for the assembler (which, incidentally, was a mere 31 instructions long). The EDSAC teleprinter alphabet was "PQWERTYUIOJ#SZK*?F@D!HNM&LXGABCV"(with "P"=00000, "Q"=00001, and so on, up to "V"=11111)
UNfortunately, the EDSAC assembler had no special directives for data values. On the other hand, there was no reason that ordinary instructions couldn't be used for this , thus, an EDSAC programmer desiring to reserve space for the constant 3/4(represented as 01100000000000000) would use the instruction "S O F" and for 1/3(which is approximately represented as 00101010101010101)"T 682 D", and so on.
Your job is to write a program that will translate decimal input value into the appropriate EDSAC instructions.
The EDSAC was programmed using a very simple assembly language: a single letter opcode followed by an unsigned decimal address, followed by the the letter "F"(for full word) or "D"(for double word). For example, the instruction "A 128 F" would mean "add the full word at location 128 to the accumulator", and would be assembled into the 17-bit binary value, 11100000100000000, consisting of a 5-bit opcode(11100="add"), an 11-bit operand (00010000000 = 128), and a single 0 bit denoting a full word operation(a 1 bit would indicate a double word operation).
Although arithmetic on the EDSAC was fixed point two's complement binary, it was not mere intger arithmetic (as is common with modern machines). The EDSAC hardware assumed a binary point between the lrftmost bit and its immediate successor. Thus the hardware could handle only values in the range -1.0 <= x < 1.0 . For example:

As you can see, the largest possible positive value was:
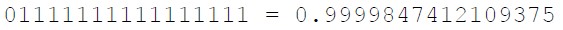
and the smallest possible positive value was:
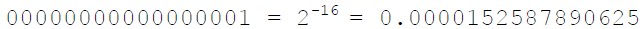
(This also happens to be the increment between successive values on the EDSAC).
By a curious coincidence(or an elegant design decision), the opcode for the add operation(11100) was the same as the teleprinter code for the letter"A". The opcode for subtract was the same as the teleprinter code for "S"(01100), and so on. This simplified the programming for the assembler (which, incidentally, was a mere 31 instructions long). The EDSAC teleprinter alphabet was "PQWERTYUIOJ#SZK*?F@D!HNM&LXGABCV"(with "P"=00000, "Q"=00001, and so on, up to "V"=11111)
UNfortunately, the EDSAC assembler had no special directives for data values. On the other hand, there was no reason that ordinary instructions couldn't be used for this , thus, an EDSAC programmer desiring to reserve space for the constant 3/4(represented as 01100000000000000) would use the instruction "S O F" and for 1/3(which is approximately represented as 00101010101010101)"T 682 D", and so on.
Your job is to write a program that will translate decimal input value into the appropriate EDSAC instructions.
Input
The frist line of input contains a single integer P,(1<=P<=1000),which is the number of data sets that follow. Each data set is a single line that contains of two space separated values N and D. N is the data set number. D is the decimal number of the from sd.ddd...., where s is an optional minus sign, and d is any decimal digit(0,-9). There will be at least 1 and at most 16 digits after the decimal point.
Output
For each data set there is one line of output. It contains the data set number(N)followed by a single space, followed by the EDSAC instruction necessary to specify the given constant. The instruction should be printed as follows:the"opcode"character followed by a space followed by the operand(as a non-negative decimal integer)followed by a space followed by an'F'or'D'(as appropriate). If the constant cannot be represented exactly in 17 bits,the value is to be rounded toward zero(up for negative,down for positive numbers). If the input value D is not in the range -1.0 <= D <= 1.0, the string"INVALID VALUE"should be printed instead of an EDSAC instruction.
Sample Input
16 1 0.5 2 -0.5 3 -1.0000000 4 0.1 5 0.0000152587890625 6 0.0000152587890624 7 0.0000152587890626 8 -0.0000152587890625 9 -0.0000152587890624 10 -0.0000152587890626 11 0.9999999999999999 12 -0.9999999999999999 13 -5.3 14 9.1 15 -1.0000000000000001 16 0.31415926
Sample Output
1 I 0 F 2 & 0 F 3 ? 0 F 4 Q 1228 D 5 P 0 D 6 P 0 F 7 P 0 D 8 V 2047 D 9 P 0 F 10 V 2047 D 11 * 2047 D 12 ? 0 D 13 INVALID VALUE 14 INVALID VALUE 15 INVALID VALUE 16 T 54 F
Source
| Home | Top |
Hangzhou Dianzi University Online Judge 3.0 Copyright © 2005-2024 HDU ACM Team. All Rights Reserved. Designer & Developer : Wang Rongtao LinLe GaoJie GanLu Total 0.000000(s) query 1, Server time : 2024-11-22 23:50:38, Gzip enabled |
Administration |