Fraction Tree

Fraction Tree ,alse called Stern-Brocot Tree.It's a beautiful way to construct the set of all nonnegative fractions.The idea is to start with irreducible fractions representing zero and infinity,
  1/0                  0/1
and then between adjacent fractions n/m and n'/m' we insert fraction (n+n')/ (m+m'), then we obtain
  1/0         1/1         0/1
Repeating the process, we get
  1/0     2/1     1/1     1/2     0/1
and then
  1/0  3/1  2/1  3/2  1/1  2/3  1/2  1/3  0/1
and so forth. It can be proven that every irreducible fraction appears at some iteration and no fraction ever appears twice . The process can be represented graphically:

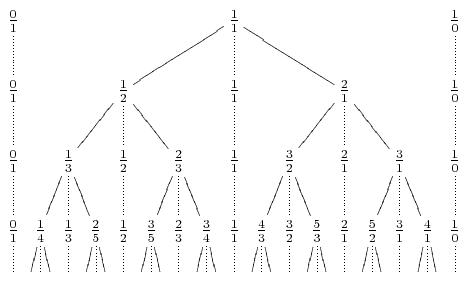
We can,in fact,regard the Stern-Brocot Tree as a number system for representing rational numbers,because each positive,reduced fractio occurs exactly once.Let's use the letters L and R to stand for going down to the left or right branch as we proceed from the root of the tree to a particular fraction; then a string of L's and R's uniquely identifies a place in the tree.For example,LRRL means that we go left from 1/1 down to 1/2,then right to 2/3,then right to 3/4,then left to 5/7.We can consider LRRL to be a representatio of 5/7. Every positive fraction gets represented in this way as a unique string of L's and R's.
There are two natural questios:
(1)Given positive integers m and n (m is coprime with n).what's the string of L's and R's that corresponds to m/n?
(2)Given a string of L's and R's,what fraction corresponds to it?
Now you need to write a problem to solve them.

The first line of input contains a single integer T - a number of test cases.
Each of the next T(T <= 1000) lines begin with a integer K(which kind of probrlem),if K = 1,following two integers M and N(M,N <= 1000000).else following a string of L's and R's(length <= 10).

For each set of data the program prints the answer.

2
1 5 7
2 LRRL

LRRL
5 7

武汉大学第五届E鸣杯程序设计大赛