Find the Difference

Big Yuer was boring at home during his winter vacation, so he started to play “Find the Difference with beautiful girls” in QQgame.

However, experts are all over the Internet! Big Yuer was beaten again and again.

The evil inside his body began to grow, he decided to make a cheater (matlab version), and he suddenly had a far sight.

This is the working cheater, and the highlighted ones are the differences.


However, he encountered some problems, which need your help.
Suppose two pictures are N*M integer matrix, we define “Trouble Rectangle” between this two as these rectangles: First, the different pixel between them must be in some “Trouble Rectangle”; second, there might be some same pixels inside a “Trouble Rectangle”, but the pixels of the outer boundary must be same in two pictures (the outer boundary means the frame “Trouble Rectangle” produces when expanding 1 pixel larger, except those out side the picture); next, a “Trouble Rectangle” cannot be included in any other “Trouble Rectangle” and cannot be intersect or adjacent to any other “Trouble Rectangle”; at last, each “Trouble Rectangle” must be unable to break down into smaller “Trouble Rectangles”.

Take two 4*4 pictures as example:

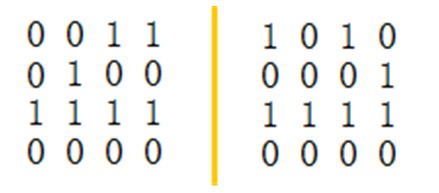
In this picture, there are two “Trouble Rectangles”, shown in below.

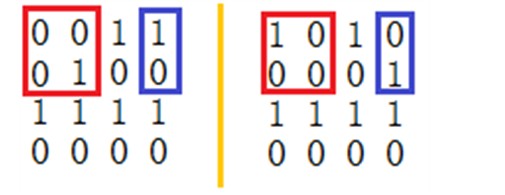
We cannot take (2,2)-(2,2) as a “Trouble Rectangle” because its outer boundary in two pictures is not same, also we cannot take (1,1)-(2,4) as “Trouble Rectangle” because it can break down into (1,1)-(2,2) and (1,4)-(2,4).
Take a 5*5 one as another example.

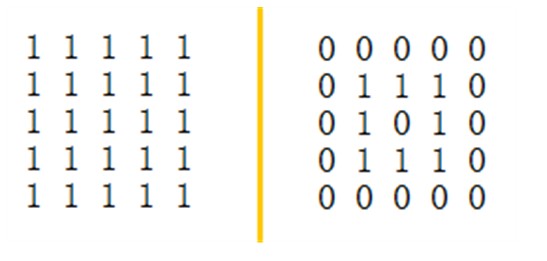
There is only one “Trouble Rectangle”, shown in the red line below.

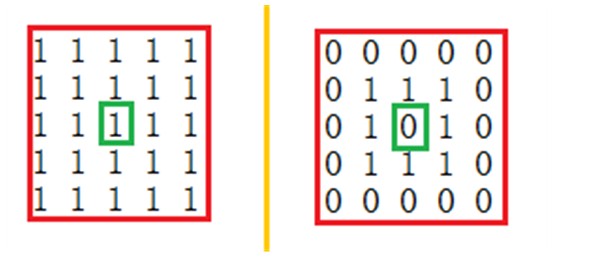
Because (3,3)-(3,3) is included in (1,1)-(5,5), so it’s not a “Trouble Rectangle”.

Multiple test cases (no more than 10), for each case:
The first line contains two integers n and m（n,m <=50）, representing height and length respectively.
Then input two n*m matrix, each number in the matrix is between 0 and 255 inclusive.

For each case:
The first line has one integer X, represent the number of “Trouble Rectangle”.
Following X line, each line output for integers xi1, yi1, xi2 and yi2, representing the coordinate of the top-left and bottom-right points. Output the one with smallest xi1 first, if there’s a tie, output the smallest yi1 first.

4 4
0 0 1 1
0 1 0 0
1 1 1 1
0 0 0 0
1 0 1 0
0 0 0 1
1 1 1 1
0 0 0 0
5 5
1 1 1 1 1
1 1 1 1 1
1 1 1 1 1
1 1 1 1 1
1 1 1 1 1
0 0 1 0 1
0 1 1 1 1
1 1 0 1 1
1 1 1 1 1
1 1 1 0 0

2
1 1 2 2
1 4 2 4
2
1 1 3 4
5 4 5 5

zhanyu

2011 Multi-University Training Contest 5 - Host by BNU