Cubic Maze

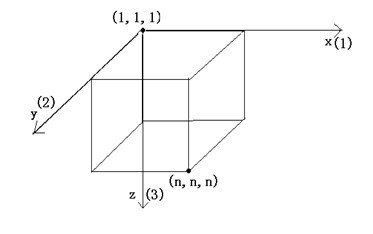
Consider an N*N*N cubic maze. We create the coordinate system as the picture below.
Now a robot is in the maze. It can be represented as a vector from his foot to head, and we call this vector the roboctor. To discribe the direction the robot will move to, we use a direct vector, which is prependicular to the roboctor. Both the roboctor and the direct vector must parallel to the coordinate axes. The robot can only be in the integral point. The robot can't go beyond the bound of the maze(i.e. The (1,1,1)->(N,N,N) space).

The robot can execute the following 6 instructions:

• F instruction. Move 1 unit along the direct vector.


• L instruction. Turn the direct vector left 90 degree around the roboctor with the roboctor unchanged.


• R instruction. Turn the direct vector right 90 degree around the roboctor with the roboctor unchanged.


• U instruction. Change the direct vector to the original roboctor and change the roboctor to the opposite of the original direct vector.


• D instruction. Change the direct vector to the opposite of the original roboctor and change the roboctor to the original direct vector.


• B instruction. Change the direct vector to the opposite of the original direct vector.

The instructions are NUMBERED FROM 1 TO 6 AS ABOVE.

There are some bombs in some integral points in the maze. The robot must avoid to move to the bomb point. For each integral point, we use 1 to represent the bomb and 0 for not. We have the map of the maze, but it is encoded. The map is encoded as follows:

Encode the N integral points with the same X coordinate and the same Z coordinate along the negative Y direction as a 0/1 string, and convert it to a 8-based number. The 8-based number is the code we get.

The entire maze can be represented by N*N 8-based numbers.

At first, the robot is at an integral point A(xa,ya,za), with direct vector DA and roboctor RA. The destination condition of the robot is to be on an integral point B(xb,yb,zb) with the direct vector DB and the roboctor RB. Your mission is to give a series of instructions to guide the robot to get to the destination condition safely(i.e. Not to hit any single bomb) with the least number of instructions.

DA, RA, DB, RB will be represented as 1~6. 1~3 represents the positive direction of X, Y, Z axis respectively. 4~6 represents the negative direction of X, Y, Z axis respectively.

An integer T comes first indicating the number of test cases. Each case contains N+3 lines:
The first line contains an integer number N (3<=N<=30) representing the cubic space.
The second line contains 5 space separated integer numbers xa,ya,za,DA,RA (1<=xa, ya, za<=N,1<=DA, RA<=6) representing the start condition.
The third line contains 5 space separated integer numbers xb,yb,zb,DB,RB (1<=xb, yb, zb<=N, 1<=DB, RB<=6) representing the destination condition.
The following N lines each contains N 8-based space separated numbers, representing the maze. The jth number of the ith line represents a line whose X coordinate is j and Z coordinate is i in the maze.

There may exist a bomb even in the start or the destination.

For each case, print one or two lines. If the robot can't get to the destination condition, print a line “Sorry, I can't get there.” (without quotes). If the robot can get to the destination condition, print two lines. The first line contains one integer indicating the least number of instructions. The second line is the instruction sequence without spaces. If there exists more than one such instruction, print the
one with the least instruction number.

2
5
1 1 1 6 4
5 5 5 6 4
0 0 0 0 0 
0 0 0 0 0 
0 0 0 0 0 
0 0 0 0 0 
0 0 0 0 0
3
1 1 1 6 5 
3 3 3 4 6 
6 0 0 
0 0 4 
0 6 2

17
RFFFFRFFFFUBFFFFU
Sorry, I can't get there.

2011 Multi-University Training Contest 4 - Host by SDU