A Hard Journey

ChenX was taken away by the arch devil, so the sharp shooter Brother Zheng was going to rescue him. The enemy’s army was distributed in an N * N grid, and each grid also can be divided in M * M small grids.

Brother Zheng's army has two kinds of attack form : from top to bottom, or from left to right. The weapon they use is Break-Cloud arrow, so each arrow will cost P fighting strength to eliminate a row or a column enemies in a big grid.

Notice that they can change the attack form at any time, and when they once change their attack form, they will use Q fighting strength.

The initial position of Brother Zheng is at the top-left corner, and ChenX was locked by arch devil at the right-bottom corner. When once make a move, Brother Zheng should eliminate all the enemies in the current big grid. If the current attack form is from top to bottom, then they can move onto the right grid of the big grid; if the current attack form is from left to right, then they can move onto the bottom grid of the big grid. The initial attack form can be either of the two.

Now Brother Zheng want to know how much the least fighting strength is so that can rescue ChenX.

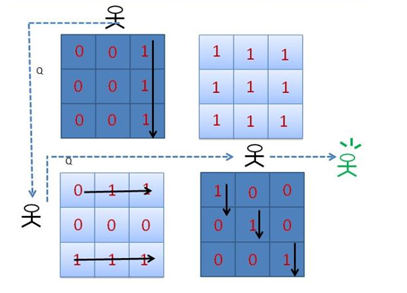
For the case as the followed picture, N = 2, M = 3, P = 2, Q = 1.
Brother Zheng choices to start with the attack form: from top to bottom. It takes P * 1 fighting strength to eliminate all the enemies at grid[1][1]. Then Brother Zheng changed attack form to “from left to right” using Q fighting strength, and moved to the bottom grid[2][1]. To eliminate all the enemies, it takes P * 2 fighting strength. Then Brother Zheng changed attack form to ”from top to bottom” using Q fighting strength, and moved to the right grid[2][2], after used P * 3 fighting strength to eliminate this grid, ChenX was rescue with P * 1 + Q + P * 2 + Q + P * 3 = 14 fighting strength.

For each case, the first line contains 4 integers: N, M, P, Q(0 < N <= 20, 0 < M <= 15, 0 <= P <= 20, 0 <= Q <= 20), the next N * N blocks, each block contains M * M matrixes, rows first.

For each case, output one integer which indicates the least fighting strength.

2 3 2 1
0 0 1
0 0 1
0 0 1
1 1 1
1 1 1
1 1 1
0 1 1
0 0 0
1 1 1
1 0 0
0 1 0
0 0 1
1 3 3 1
0 0 1
0 0 1
1 1 1

14
7

2011 Multi-University Training Contest 3 - Host by BIT