
| Online Judge | Online Exercise | Online Teaching | Online Contests | Exercise Author |
|
F.A.Q Hand In Hand Online Acmers |
Best Coder beta VIP | STD Contests DIY | Web-DIY beta |
Factorial Simplification
Time Limit: 4000/2000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)Total Submission(s): 706 Accepted Submission(s): 250
Problem Description
Peter is working on a combinatorial problem. He has carried out quite lengthy derivations and got a resulting formula that is a ratio of two products of factorials like this:
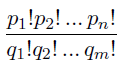
This does not surprise Peter, since factorials appear quite often in various combinatorial formulae, because n! represents the number of transpositions of n elements - one of the basic combinatorial objects.
However, Peter might have made a mistake in his derivations. He knows that the result should be an integer number and he needs to check this first. For an integer result Peter wants to simplify this formula to get a better feeling of its actual combinatorial significance. He wants to represent the same number as a product of factorials like this.
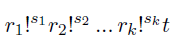
where all ri are distinct integer numbers greater than one in the descending order (ri > ri+1 > 1), si and t are positive integers. Among all the possible representations in this form, Peter is interested in one where r1 is the largest possible number, among those in the one where s1 is the largest possible number; among those in the one where r2 is the largest possible number; among those in the one where s2 is the largest possible number; etc, until the remaining t cannot be further represented in this form. Peter does not care about the actual value of t. He wants to know what is the factorial-product part of his result.
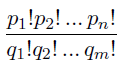
This does not surprise Peter, since factorials appear quite often in various combinatorial formulae, because n! represents the number of transpositions of n elements - one of the basic combinatorial objects.
However, Peter might have made a mistake in his derivations. He knows that the result should be an integer number and he needs to check this first. For an integer result Peter wants to simplify this formula to get a better feeling of its actual combinatorial significance. He wants to represent the same number as a product of factorials like this.
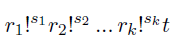
where all ri are distinct integer numbers greater than one in the descending order (ri > ri+1 > 1), si and t are positive integers. Among all the possible representations in this form, Peter is interested in one where r1 is the largest possible number, among those in the one where s1 is the largest possible number; among those in the one where r2 is the largest possible number; among those in the one where s2 is the largest possible number; etc, until the remaining t cannot be further represented in this form. Peter does not care about the actual value of t. He wants to know what is the factorial-product part of his result.
Input
The input begins with an integer T. The next T blocks each represents a case. The first line of each case contains two integer numbers n and m (1 ¡Ü n, m ¡Ü 1000). The second line contains n integer numbers pi (1 ¡Ü pi ¡Ü 10 000) separated by spaces. The third line contains m integer numbers qi (1 ¡Ü qi ¡Ü 10 000) separated by spaces.
Output
For each case, on the first line of the output write a single integer number k. Write k = -1 if the ratio of the given factorial products is not an integer. Write k = 0 if the ratio is an integer but it cannot be represented in the desired form. Write k > 0 followed by k lines if the ratio can be represented by a factorial product as described in the problem statement. On each of the following k lines write two integers ri and si (for i = 1 ... k) separated by a space.
Sample Input
3 1 2 6 4 4 1 2 6 3 4 4 2 9 2 2 2 3 4
Sample Output
-1 0 2 7 1 2 2
Author
Andrey Stankevich
Source
| Home | Top |
Hangzhou Dianzi University Online Judge 3.0 Copyright © 2005-2025 HDU ACM Team. All Rights Reserved. Designer & Developer : Wang Rongtao LinLe GaoJie GanLu Total 0.001000(s) query 1, Server time : 2025-02-02 10:00:30, Gzip enabled |
Administration |