Evaluating Functions

A teleport machine - a special kind of machine capable of moving objects from one place to another instantaneously, without passing through the intervening space - has just been invented. Out of curiosity, you went to the laboratory and asked if you could have a try. Although even the engineers who have designed this machine can't control where the object entering the machine will end up, they have told you the way the teleport machine operates:



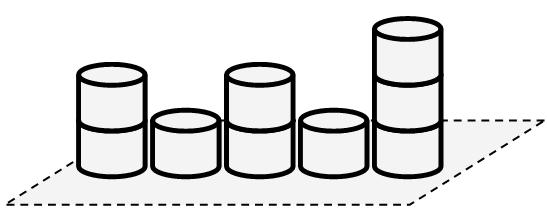
In the interior of the teleport machine you may find a special structure (as illustrated above). There are N cylinders of possibly different integer heights, and a special (yet unknown to you) value had been assigned to each of them in the following way:

Suppose the heights of the cylinders are recorded in the array H[] , the values assigned to them are recorded in the array value[] , and we are currently calculating the value for cylinder X (i.e., valuex . Before this process is executed, valuex will be set to zero, and we initialized a pointer, P , which should be pointing to X at the beginning)


0.
Let P = P - 1 . (i.e., modifies the pointer P so that it now points to the cylinder on the left side of the current cylinder P ). If there's none (P = = NULL) , or Hp > Hx , then let P = X , and go to step 2; otherwise, proceed to the next step.
1.
Find the highest cylinder on the left side of the cylinder P , and let its height be H' . If such cylinder exists, increase valuex by max{min{H', Hx} - Hp, 0} , and go to step 0.
2.
Let P = P + 1 . (i.e., modifies the pointer P so that it now points to the cylinder on the right side of the current cylinder P ). If there's none (P = = NULL) , or Hp > Hx , then terminate the process; otherwise, proceed to the next step.
3.
Find the highest cylinder on the right side of the current cylinder P , and let its height be H' . If such cylinder exists, increase valuex by max{min{H', Hx} - Hp, 0} , and go to step 2.


You have to enter two integers, the distance which you want to move the object, K , and the K -th largest value T among all N cylinders' values. A serious malfunction will occur unless the numbers K and T are entered correctly. (It is easy to see that if we follow the process described above strictly, it takes O(N3) time to calculate all values; that is why the engineers can only use short-distance teleportation so far; however you wonder whether there exists a way to evaluate the function effectively so as to use the long-range transfer ability of this machine.)

Now you have to figure out what the value of T is, given the heights of all cylinders of the teleport machine and the distance you need to move the object. For example you find the machine has 5 cylinders, and the distance you want to move the object is 2. Their heights are 2 1 2 1 3 so your calculations (value ) are 2 0 2 0 2. After that the T which you should enter the second largest value is 2.

There are multiple test cases in the input file. Each test case starts with two integers N and K (1<=N<=2×105, 1<=K<=N) , the number of cylinders on the teleport machine, and the distance you want to move the object, respectively. Each of the following N lines contains one integer P (1<=P<=10^6) , the integer on the i -th line representing the height of the i -th cylinder. There is a blank line after each test case. A single line with N = 0 , K = 0 indicates the end of input file.

For each test case, output one integer, the number you have to enter, in the format as indicated in the sample output.

5 2 
2 
1 
2 
1 
3 

5 1 
4
5 
1 
1 
7 

0 0

Case 1: 2 
Case 2: 8

2007 Asia Regional Chengdu