
| Online Judge | Online Exercise | Online Teaching | Online Contests | Exercise Author |
|
F.A.Q Hand In Hand Online Acmers |
Best Coder beta VIP | STD Contests DIY | Web-DIY beta |
Jacobi symbol
Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)Total Submission(s): 942 Accepted Submission(s): 411
Problem Description
Consider a prime number p and an integer a !°‘ 0 (mod p). Then a is called a quadratic residue mod p if there is an integer x such that x2 °‘ a (mod p), and a quadratic non residue otherwise. Lagrange introduced the following notation, called the Legendre symbol, L (a,p):
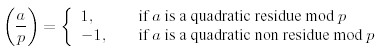
For the calculation of these symbol there are the following rules, valid only for distinct odd prime numbers p, q and integers a, b not divisible by p:
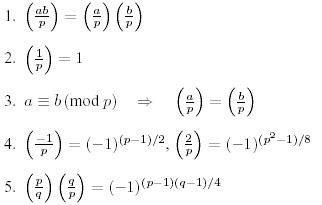
The Jacobi symbol, J (a, n) ,is a generalization of the Legendre symbol ,L (a, p).It defines as :
1. J (a, n) is only defined when n is an odd.
2. J (0, n) = 0.
3. If n is a prime number, J (a, n) = L(a, n).
4. If n is not a prime number, J (a, n) = J (a, p1) *J (a, p2)°≠* J (a, pm), p1°≠pm is the prime factor of n.
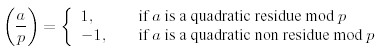
For the calculation of these symbol there are the following rules, valid only for distinct odd prime numbers p, q and integers a, b not divisible by p:
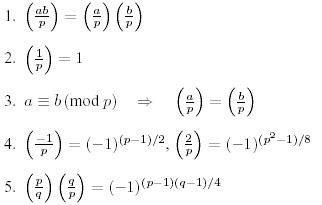
The Jacobi symbol, J (a, n) ,is a generalization of the Legendre symbol ,L (a, p).It defines as :
1. J (a, n) is only defined when n is an odd.
2. J (0, n) = 0.
3. If n is a prime number, J (a, n) = L(a, n).
4. If n is not a prime number, J (a, n) = J (a, p1) *J (a, p2)°≠* J (a, pm), p1°≠pm is the prime factor of n.
Input
Two integer a and n, 2 < a< =106£¨2 < n < =106£¨n is an odd number.
Output
Output J (a,n)
Sample Input
3 5 3 9 3 13
Sample Output
-1 0 1
Author
alpc41
Source
| Home | Top |
Hangzhou Dianzi University Online Judge 3.0 Copyright © 2005-2024 HDU ACM Team. All Rights Reserved. Designer & Developer : Wang Rongtao LinLe GaoJie GanLu Total 0.000000(s) query 1, Server time : 2024-11-23 16:13:24, Gzip enabled |
Administration |