
| Online Judge | Online Exercise | Online Teaching | Online Contests | Exercise Author |
|
F.A.Q Hand In Hand Online Acmers |
Best Coder beta VIP | STD Contests DIY | Web-DIY beta |
Code
Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)Total Submission(s): 156 Accepted Submission(s): 10
Problem Description
A new code system was designed recently. It works in the following way:
The original code A is a linear sequence containing N elements. Each element is an integer between 1 and N. At first the code system will generate a permutation B of length N automatically. Compare sequence A and B we can compute a hidden code C by the following rule:
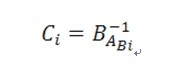
where, B-11 stands for the location of integer i in permutation B. For example, if B = {3, 1, 2}, we have B-11=2,B-13=1 .
The code system has many great advantages in security. For instance, hackers will not have any idea about the original code A if he only gets the hidden code C. Considering all of these, we ordered one of the code systems.
However, some awful thing happened yesterday, the boss totally forgot his original code! The boss has the record of his hidden code, and he wants to ask you if it¡¯s possible for him to find the original code soon.
More exactly, your task is to count the number of possible original codes that may generate the hidden code C by some permutation B.
The original code A is a linear sequence containing N elements. Each element is an integer between 1 and N. At first the code system will generate a permutation B of length N automatically. Compare sequence A and B we can compute a hidden code C by the following rule:
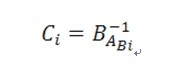
where, B-11 stands for the location of integer i in permutation B. For example, if B = {3, 1, 2}, we have B-11=2,B-13=1 .
The code system has many great advantages in security. For instance, hackers will not have any idea about the original code A if he only gets the hidden code C. Considering all of these, we ordered one of the code systems.
However, some awful thing happened yesterday, the boss totally forgot his original code! The boss has the record of his hidden code, and he wants to ask you if it¡¯s possible for him to find the original code soon.
More exactly, your task is to count the number of possible original codes that may generate the hidden code C by some permutation B.
Input
The input contains multiple test cases.
In the first line of the input there¡¯s an integer T which is the number of test cases. Then the description of T test cases will be given.
For each test case there will be two lines. The first line contains one integer N (¡Ü 30) which is the length of the hidden code C. The second line contains N integers between 1 and N giving C.
In the first line of the input there¡¯s an integer T which is the number of test cases. Then the description of T test cases will be given.
For each test case there will be two lines. The first line contains one integer N (¡Ü 30) which is the length of the hidden code C. The second line contains N integers between 1 and N giving C.
Output
For each test case, output one line containing exactly one integer, the number of different original codes that may generate C. Take a look at the sample output for format.
Sample Input
3 5 1 2 3 4 5 5 2 2 2 2 2 5 3 2 5 2 2
Sample Output
Case 1: 1 Case 2: 5 Case 3: 120
Source
| Home | Top |
Hangzhou Dianzi University Online Judge 3.0 Copyright © 2005-2024 HDU ACM Team. All Rights Reserved. Designer & Developer : Wang Rongtao LinLe GaoJie GanLu Total 0.000000(s) query 1, Server time : 2024-11-25 13:08:28, Gzip enabled |
Administration |