Catch

A thief is running away!
We can consider the city where he locates as an undirected graph in which nodes stand for crosses and edges stand for streets. The crosses are labeled from 0 to N–1.
The tricky thief starts his escaping from cross S. Each moment he moves to an adjacent cross. More exactly, assume he is at cross u at the moment t. He may appear at cross v at moment t + 1 if and only if there is a street between cross u and cross v. Notice that he may not stay at the same cross in two consecutive moment.
The cops want to know if there’s some moment at which it’s possible for the thief to appear at any cross in the city.

The input contains multiple test cases:
In the first line of the input there’s an integer T which is the number of test cases. Then the description of T test cases will be given.
For any test case, the first line contains three integers N (≤ 100 000), M (≤ 500 000), and S. N is the number of crosses. M is the number of streets and S is the index of the cross where the thief starts his escaping.
For the next M lines, there will be 2 integers u and v in each line (0 ≤ u, v < N). It means there’s an undirected street between cross u and cross v.

For each test case, output one line to tell if there’s a moment that it’s possible for the thief to appear at any cross. Look at the sample output for output format.

2
3 3 0
0 1
0 2
1 2
2 1 0
0 1

Case 1: YES
Case 2: NO

For the first case, just look at the table below. (YES means the thief may appear at the cross at that moment)

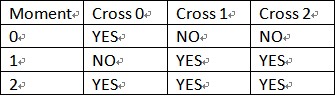
For the second input, at any moment, there’s at least one cross that the thief can’t reach.

2010 ACM-ICPC Multi-University Training Contest（5）——Host by BJTU